Понятие о решении задач нестационарной теплопроводности
Тепловые процессы называются нестационарными, если температурное поле системы, в которой протекает теплообмен, изменяется по времени.
 Нестационарные процессы теплопроводности имеют место в теплонапряженных элементах тепловых машин при их запуске, выключении или при изменении режима работы. Кроме того, нестационарная теплопроводность характерна для сооружений незащищенного грунта при суточном изменении температуры, для большего количества технологических процессов и многих теплообменных устройств. На рис.6.5 показан временной характер изменения температур двух точек твердого тела, нагреваемого в среде с постоянной температурой Тср.
Нестационарные процессы теплопроводности имеют место в теплонапряженных элементах тепловых машин при их запуске, выключении или при изменении режима работы. Кроме того, нестационарная теплопроводность характерна для сооружений незащищенного грунта при суточном изменении температуры, для большего количества технологических процессов и многих теплообменных устройств. На рис.6.5 показан временной характер изменения температур двух точек твердого тела, нагреваемого в среде с постоянной температурой Тср.
По мере прогрева тела температура в каждой точке асимптотически приближается к температуре нагревающей среды. Наиболее быстро изменяется температура точек поверхности (кривая 1). Точки, лежащие внутри тела (кривая 2), будут прогреваться с некоторым запаздыванием.
Решить задачу нестационарной теплопроводности – значит найти для заданной точки тела величину температуры и количество теплоты в искомый момент времени. Исходными уравнениями задачи нестационарной теплопроводности являются дифференциальное уравнение (6.8)
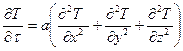
и условия однозначности, заданные в виде:
–теплофизических свойств тела  cp ;
cp ;
– формы и геометрических размеров тела Ф, l ;
– температуры тела в начальный момент времени при 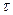 = 0
= 0
Тс т= Т0= f (xст, yст, zcn, );
– граничных условий III рода 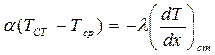 .
.
Дифференциальное уравнение и условия однозначности дают законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании функции
T=f(x, y, z, 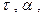 cp,
cp, 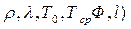 ,
,
которая удовлетворяла бы исходному уравнению и условиям однозначности.
Отсюда видно, что температура зависит в общем виде от большого числа переменных и постоянных параметров, и определение ее представляет сложную математическую задачу. В зависимости от условий однозначности и требуемой точности разработаны и используются различные методы решения, которые можно разделить на следующие группы:
– аналитические методы;
– численные методы;
– методы аналогий.
К аналитическим методам отнесем решения задач нестационарной теплопроводности, не требующие машинной или аналогичной ей техники. Некоторые из этих методов изложены, например, в [4, 7].
В настоящее время наиболее распространены численные методы решения задач нестационарной теплопроводности. Постановка задач, используемые программы, алгоритмы решений приводятся в ряде работ, например, в [4, 6.7].
Дата добавления: 2015-08-04; просмотров: 1111;
