Граничные условия. Для решения данной задачи используем граничные условия I рода, т.е

Для решения данной задачи используем граничные условия I рода, т.е. при x = 0, T = T_{cm 1} ; при x = δ, T = T_{cm 2}.

Необходимо определить характер изменения температуры в плоской стенке, т.е. T=f(x) и получить формулу плотности теплового потока.

Исходное уравнение (6.8) при условиях однозначности будет иметьследующий вид:

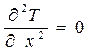(6.9)

Рис. 6.3

Первое интегрирование уравнения (6.9) дает 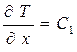. После второго интегрирования получим: T = C1 x +C2 (6.10) Здесь C1 и C2 – постоянные, которые определяются из граничных условий. Так, при x = 0, T = Tcm 1 постоянная C2 = Tcm 1 ; при x = δ, T = Tcm 2, отсюда C1 = (Tcm 2 – Tcm 1) / δ . Подставляя значения постоянных С1 и С2 в выражение (6.10), получим уравнение, устанавливающее изменение температуры по толщине плоской стенки для случая Tcm 1>Tcm 2: 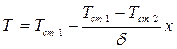(6.11) Из уравнения (6.11) следует, что при постоянном коэффициенте теплопроводности температура в стенке изменяется по линейному закону; в координатах T x она изобразится

прямой линией от T_{cm 1} до Т_{cm 2 ,} (см. рис 6.3).

Для определения плотности теплового потока, проходящего через стенку в направлении оси x, воспользуемся законом Фурье, согласно которому

.

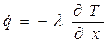Заменим ∂Т/∂x значением С₁, получим:

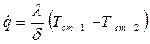. (6.12)

Анализ уравнения (6.12) показывает, что количество тепла, проходящее через единицу поверхности стенки в единицу времени, прямо пропорционально коэффициенту теплопроводности и разности температур на наружных поверхностях стенки и обратно пропорционально толщине стенки.

Разность температур (Т_ст1 - T_cm2) принято называть т е м п е р а-атурным напором. Отношение λ/δ называют тепловой проводимостью, аобратную ей величину δ/λ – термическим сопротивлением.

Используя уравнения (6.11) и (6.12), получим выражение:

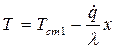, (6.13)

которое устанавливает характер распределения температуры по толщине стенки при известных граничных условиях I и II рода.

6.3.2. Теплопроводность плоской многослойной стенки

В теплонапряженных конструкциях энергетических установок часто встречаются стенки, состоящие из нескольких плоских слоев различных материалов и различной толщины. Получим уравнение плотности теплового потока через многослойную стенку, полагая контакт между слоями настолько плотным, что температура на соприкасающихся поверхностях двух смежных слоев одинакова.

Характерной особенностью распространения теплоты при стационарном режиме является то, что плотность теплового потока не зависит от координаты, т.е. величина q для любого слоя стенки одна и та же.

Решение поставленной задачи рассмотрим на примере трехслойной плоской стенки (рис. 5.5).

Уравнения плотности теплового потока для каждого слоя стенки запишем аналогично выражению (6.12) в виде системы: 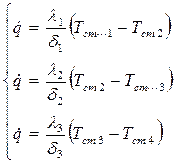Из этих уравнений определим температурные напоры в каждом слое

Рис. 6.4

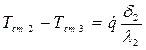и .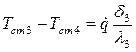

Сложив, левые и правые части этих равенств, получим:

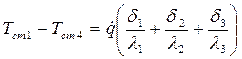
или

.

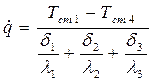Для многослойной стенки, состоящей из n слоев, формула плотности теплового потока будет иметь вид:

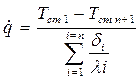(6.14)

Для многослойной стенки с различными коэффициентами теплопроводности слоев температурный график представляет собой ломаную линию, (см. рис. 6.4).

Для вычисления теплового потока через однослойную цилиндрическую стенку (например, трубу) используется следующее уравнение:

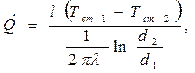(6.15)

где l – длина трубы;

d₁ и d₂ – внутренний и наружный диаметры трубы.