Теплоотдача
7.1.1.Основной закон теплоотдачи
Понятие конвективного теплообмена охватывает процесс переноса теплоты конвекцией между твердыми поверхностями и омывающими их теплоносителями. Теплоносителем, как правило, является либо жидкость, либо газ. Однако в качестве теплоносителей могут использоваться двух- или трехфазные системы: газ – жидкость; газ – твердые частицы; газ – жидкость – твердые частицы.
В теплоносителе с неоднородным полем температур при вынужденном или естественном перемещении макроскопических элементов наряду с конвекцией происходит процесс переноса тепла теплопроводностью.
Совместный процесс конвекции и теплопроводности называют конвективным теплообменом.
Конвективный теплообмен протекает как внутри теплоносителя, так и на границах его соприкосновения с поверхностями обтекаемых тел.
Конвективный теплообмен между теплоносителем и поверхностью обтекаемого им тела называют теплоотдачей.
Обычно в инженерной практике исследуют теплоотдачу, конвективный же теплообмен внутри теплоносителя при этом не рассматривается.
Тепловой поток при теплоотдаче всегда направлен в сторону меньшей температуры. В процессе теплоотдачи плотность теплового потока, согласно закону Ньютона, прямо пропорциональна температурному напору между теплоносителем и поверхностью теплообмена, т.е.
 (7.1)
(7.1)
где α – коэффициент пропорциональности, называемый к о э ф ф и ц и е н-
т о м т е п л о о т д а ч и;
∆Т – температурный напор.
При Tm >Tcm это ∆T = Tm - Tcm ; если Tc m> Tm, то ∆T = Tcm - Tm .
Здесь индексом m обозначена температура теплоносителя, индексом cm
– температура поверхности теплообмена (стенки).
Для произвольной поверхности при Tm > Tcm закон Ньютона запишется в виде:
 . (7.2)
. (7.2)
Значения F, Tm и Tcm в уравнении (6.2) не отражают условий теплообмена, влияющих на величину 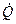 . Здесь α не является физической постоянной, присущей данному теплоносителю, а зависит от множества факторов, формирующих картину течения около стенки. По этой причине простота уравнения (7.1) представляется кажущейся, и особенности его использования заключаются в сложности определения коэффициента теплоотдачи.
. Здесь α не является физической постоянной, присущей данному теплоносителю, а зависит от множества факторов, формирующих картину течения около стенки. По этой причине простота уравнения (7.1) представляется кажущейся, и особенности его использования заключаются в сложности определения коэффициента теплоотдачи.
7.1.2. Факторы, влияющие на коэффициент теплоотдачи.
Величина коэффициента теплоотдачи характеризует интенсивность конвективного теплообмена на границе “теплоноситель-стенка”.
Численно коэффициент теплоотдачи равен тепловому потоку, приходящемуся на единицу поверхности при температурном напоре, равный единице, т.е.
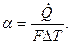
Отсюда же следует и единица α – Вт/(м2 × К).
Коэффициент теплоотдачи имеет весьма широкий диапазон численных значений, табл. 7.1.
Таблица 7.1
| Особенности теплоотдачи |  . .
|
| Естественная конвекция газов | 6…40 |
| Вынужденное движение газов | 12…120 |
| Вынужденное движение пара в трубах | 110…2200 |
| Естественная конвекция воды | 110…1100 |
| Вынужденное движение воды | 500…11000 |
| Пузырьковое кипение воды | 8500…18000 |
| Конденсация водяного пара | 4500…22000 |
На величину коэффициента теплоотдачи влияют, прежде всего, теплофизические свойства теплоносителя, его фазовое состояние, вид движения (естественное или вынужденное) и режим течения теплоносителя. Различают ламинарный, переходный и турбулентный режимы течения.
При ламинарном (слоистом) режиме макрочастицы жидкости движутся, не перемешиваясь, параллельно омываемым стенкам и траекториям других частиц. В силу внутреннего трения скорость теплоносителя переменна по сечению нормальному к поверхности. Так, для канала круглого сечения эпюра скорости имеет параболическую форму, рис.7.1, а Перенос тепла при ламинарном режиме движения происходит в осноном за счет теплопроводности теплоносителя и естественной конвекции.
При турбулентном режиме макрочастицы перемещаются по сложным траекториям, не совпадающим с общим направлением потока. Их движение неупорядоченное, хаотичное. Эпюра скорости имеет вид усеченной параболы, (см. рис. 7.1, б). Теплоотдача при турбулентном режиме течения теплоносителя отличается несравненно большей интенсивностью, чем при ламинарном режиме
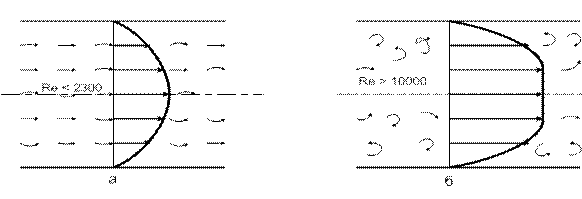
Рис. 7.1
Как при ламинарном, так и при турбулентном режимах движения скорость теплоносителя непосредственно на стенке равна нулю, а с увели -чением расстояния по нормали от стенки она возрастает.
Слой теплоносителя около поверхности тела, где скорость изменяется от нуля до величины, примерно равной 0,9 скорости невозмущенного потока, называют г и д р о д и н а м и ч е с к и м пограничным слоем и обозначают буквой δд , рис.7.2.

а б в
Рис. 7.2
Кроме того, необходимо отметить, что в турбулентном пограничном слое непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором имеет ламинарный характер. Этот слой называют вязким, или л а м и н а р н ы м п о д с л о е м и обозначают δл (см. рис. 7.2, б).
Если температуры стенки и теплоносителя не одинаковы, то вблизи стенки образуется тепловой пограничный слой δт (см. рис.7.2, в). В нем температура изменяется от Tcm до ≈ Tm , т.е. все изменение температуры происходит в сравнительно тонком слое, непосредственно прилегающем к поверхности теплоотдачи. Значения толщин δд и δт в общем случае не равны, соотношение между ними зависит от рода жидкости. Однако изменения в δд приводят к изменениям δт. С увеличением скорости теплоносителя значения толщин δд , δт и δл уменьшаются.
При вынужденной конвекции режим течения оценивают по безразмерному комплексу, называемому критерием Рейнольдса. Для цилиндрического канала критерий Рейнольдса имеет вид:
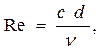
где c - скорость течения теплоносителя,;
d - диаметр канала,;
ν - коэффициент кинематической вязкости,.
Течение теплоносителя в трубах принято считать ламинарным до
Re < 2300. В диапазоне 2300 > Re < 10000 наблюдается переходный режим течения (от ламинарного к турбулентному). При Re > 10000 течение турбулентное.
Для того, чтобы качественно оценить влияние режима течения теплоносителя на коэффициент теплоотдачи, запишем уравнение теплоотдачи в дифференциальной форме.
Для слоя теплоносителя непосредственно на поверхности теплообмена по закону Фурье следует:
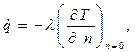
где n – нормаль к поверхности тела,.
С другой стороны, согласно закону Ньютона,
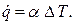
Приравнивая правые части этих уравнений, получим:
 (7.3)
(7.3)
Уравнение (7.3) выражает условия теплоотдачи на границе “твердая стенка – теплоноситель”.
Чем больше скорость движения теплоносителя, тем меньше толщина пограничного слоя, тем больше градиент температуры и, следовательно, больше коэффициент теплоотдачи. Через толщину пограничного слоя на 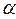 влияют форма и размер поверхности теплообмена.
влияют форма и размер поверхности теплообмена.
Величина коэффициента теплоотдачи зависит от физических свойств теплоносителя.С увеличением плотностиρ, теплопроводности λ, теплоем-кости cpи уменьшением вязкости ν коэффициент теплоотдачи возрастает.
Влияние температур Tm и Tcm на 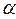 сказывается через их воздействие на физические свойства теплоносителя.
сказывается через их воздействие на физические свойства теплоносителя.
Таким образом, в самом общем виде коэффициент теплоотдачи является функцией многих факторов:
α = f(X, Ф, l, c, ν, ρ, λ, cp, Tm, Tcm, …), (7.4)
где X – характер движения теплоносителя;
Ф – форма поверхности теплообмена;
l – характерный геометрический размер;
c – скорость движения теплоносителя.
Для определения коэффициента теплоотдачи в зависимости от поста-
новки задачи могут использоваться следующие методы: экспериментальный,
аналитический и метод теплового подобия.
Чисто экспериментальный метод определения коэффициента теплоотдачи весьма прост и достоверен, так как требует опытного измерения
только трех величин: 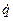 , Tm и Tcm. Отсюда
, Tm и Tcm. Отсюда
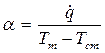 .
.
Этот метод широко используется при исследовании влияния различных факторов на интенсивность теплоотдачи в функционирующих теплообменных установках. Однако экспериментальный метод имеет существенный недостаток, состоящий в том, что полученное значение α не может быть рекомендовано для использования при расчетах устройства, характеристики которого хотя бы незначительно отличаются от характеристик опытной установки.
Аналитические методы основаны на теории пограничного слоя. Сущность этих методов состоит в составлении замкнутой системы дифференциальных уравнений, описывающих процесс конвективного теплообмена в движущемся теплоносителе и последующем решении этой системы. Дифференциальные уравнения, описывающие конвективный теплообмен, устанавливают самую общую связь между величинами, характерными для этого процесса. Следовательно, эти дифференциальные уравнения являются математической моделью целого класса процессов теплообмена. Для получения частного решения эти уравнения дополняются условиями однозначности.
В большинстве случаев, из-за сложности математического описания профиля скорости в пограничном слое, решения, удовлетворяющие дифференциальным уравнениям и условиям однозначности, весьма трудоемки.
Следовательно, если недостатком экспериментального метода определения α является невозможность распространения результатов опытов на другие условия теплообмена, отличающиеся от изученного, то недостатком аналитического метода является невозможность перейти от класса явлений конвективного теплообмена, характеризующегося дифференциальными уравнениями, к единичному, конкретному явлению. Каждый из этих методов в отдельности не может быть эффективно использован для решения практических задач.
В настоящее время для определения коэффициента теплоотдачи в основном используется метод теплового подобия, который объединяет в себе положительные стороны экспериментального и аналитического методов.
Дата добавления: 2015-08-04; просмотров: 3324;
