Тема 7. Матричные функции

В категории математических функций имеются функции, которые реализуют средства линейной алгебры. Их аргументами являются матрицы, которые могут быть заданы адресами, именами, массивами констант. К таким функциям относятся:

ТРАНСП(матрица) – транспонирует исходную прямоугольную матрицу, т.е. меняет элементы ее строк и столбцов местами.

Например, матрица 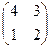после транспонирования будет иметь вид: .

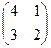=ТРАНСП(А2:В3) – транспонирует матрицу, помещенную в блок ячеек А2:В3, в выделенный блок ячеек (на рис. 51 в блок ячеек Е5:F6).

МОПРЕД(матрица) – вычисляет определитель прямоугольной матрицы.

Например,

det A = 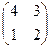= 4∙2 – 3∙1 = 5

=МОПРЕД(А2:В3) – вычислит определитель матрицы, записанной в блок ячеек А2:В3, и поместит в ячейку I5, где записана эта функция (рис. 51).

МОБР(матрица) – вычисляет матрицу, обратную к данной. Исходная и полученная матрицы могут быть только квадратными, т.е. имеющими одинаковое число строк и столбцов. Перемножение обратной и прямой матриц дает единичную матрицу, т.е. матрицу, у которой на главной диагонали находятся единицы. Не все матрицы имеют обратную. В этом случае будет выдано сообщение об ошибке #ЧИСЛО!.

=МОБР(А2:В3) – вычислит матрицу, обратную матрице, записанной в блок ячеек и поместит ее в выделенный диапазон (на рис. 51 – в блок ячеек E2:F3).

МУМНОЖ(матрица1; матрица2) – перемножает матрицы-аргументы и помещает их в выделенный блок ячеек. Число столбцов матрицы 1 должно совпадать с числом строк матрицы 2. Результирующая матрица будет иметь число строк, как и матрица 1, и число столбцов, как матрица 2.

Например, функция

=МУМНОЖ(A2:B3;E2:F3)

перемножить матрицы, находящиеся в блоках ячеек A2:B3 и E2:F3 и поместит в блок ячеек I2:J3. Так как матрицы, находящиеся в блоках ячеек A2:B3 и E2:F3 соответственно прямая и обратная, то в результате их перемножения получилась единичная матрица показанная на рисунке 251.

Рисунок 251

Для ввода одной из функций: ТРАНСП(матрица), МОБР(матрица), МУМНОЖ(матрица1; матрица2) должны быть выполнены следующие действия:

- выделен блок ячеек, куда должны быть помешены результаты;

- в текущую ячейку введена функция;

- нажата комбинация клавиш Shift+Ctrl+Enter (в строке формул введенная формула автоматически обрамляется в фигурные скобки).

Рассмотрим пример.

Дана матрица А = 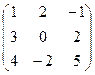. Используя матричные функции, вычислить обратную матрицу, транспонировать матрицу А, вычислить определитель матрицы, умножить обратную матриц на прямую.

1. Откройте новый лист рабочей книги Excel и назовите его «Матричные функции».

2. В блок ячеек А4:С6 введите матрицу А рисунок 252.

Рисунок 252

Разместите обратную матрицу в блоке Е4:G6. Для получения обратной матрицы:

- выделите блок ячеек Е4:G6;

- в текущую ячейку блока введите формулу =МОБР(А4:С6);

- нажмите клавиши Shift+Ctrl+Enter.

Поместите транспонированную матрицу в блок ячеек Е8:G10. Для получения транспонированной матрицы:

- выделите блок ячеек Е8:G10;

- в текущую ячейку блока введите формулу =ТРАНСП(А4:С6);

- нажмите клавиши Shift+Ctrl+Enter.

После выполнения указанных действий в режиме показа формул блоки ячеек Е4:G6 и Е8:G10 будут иметь вид показанный на рисунке 253.

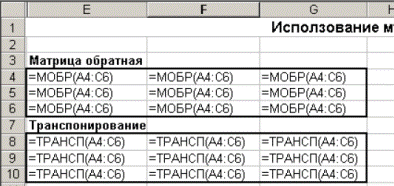
Рисунок 253

Для размещения результата произведения прямой и обратной матриц используем блок ячеек I4:K6. Для нахождения произведения матриц:

- выделите блок ячеек I4:K6;

- в текущую ячейку введите формулу =МУМНОЖ(А4:С6; E4:G6);

- нажмите клавиши Shift+Ctrl+Enter как показано на рисунке 254 – в режиме показа формул.

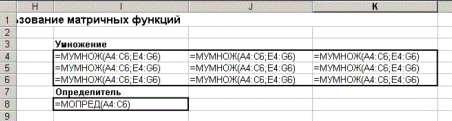
Рисунок 254

Для вычисления определителя матрицы в ячейку I8 введите формулу =МОПРЕД(А4:С6). В результате в режиме решения таблица будет иметь вид показанный на рисунке 255.

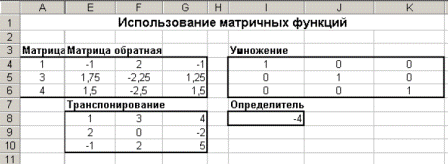
Рисунок 255

Пример. Используя матричные функции, составить таблицу для решения системы уравнений

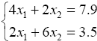
В матричной форме система уравнений может быть записана следующим образом:

А·Х = В,

где А – матрица коэффициентов системы, Х – вектор-столбец неизвестных, В – вектор-столбец свободных членов:

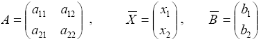
Для решения матричных уравнений удобно использовать обратную матрицу. Если det ≠ 0, можно вычислить обратную матрицу А^-1 и умножить левую и правую части заданного уравнения слева на А^-1:

А^-1·(А·Х) = А^-1·В.

Так как А^-1·(А·Х) = (А^-1·А)·Х, то А^-1·(А·Х) = E·X = X. Тогда получаем

X = А^-1·B.

Таким образом, для нахождения решения (вектора-столбца Х) надо найти обратную матрицу А^-1 и умножить ее на вектор-столбец В.

Выполните следующие действия:

- Откройте новый лист рабочей книги и назовите его Решение системы уравнений.

- В блок ячеек А2:В3 введите коэффициенты системы уравнений.

- В блок ячеек D2:D3 введите элементы вектор-столбца свободных членов.

- Выделите блок ячеек F2:G3; в текущую ячейку блока введите =МОБР(А2:В3); нажмите кнопки Shift+Ctrl+Enter.

- Выделите блок ячеек G5:G6; в текущую ячейку блока введите =МУМНОЖ(F2:G3;D2:D3); нажмите кнопки Shift+Ctrl+Enter.

- Введите пояснительный текст, как показано на рисунке 256.

Рисунок 256

Получите решение системы уравнений в ячейках G5:G6 рисунок 257.

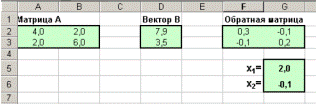
Рисунок 257