Продольно-поперечный изгиб
Рассмотрим шарнирно опертую по концам балку (рис.1), которая находится под действием поперечной нагрузки и центрально приложенной силы Р.
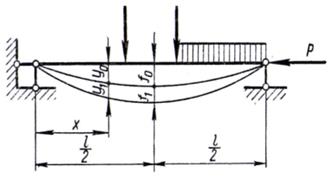
Рис. 1
Допустим, что сначала действовала только поперечная нагрузка, которая вызвала изгиб балки. Обозначим через у0 и М0 прогиб и изгибающий момент в любом сечении балки и примем это состояние за начальное.
Приложим теперь к стержню, имеющему предварительное начальное искривление, сжимающую силу Р, тогда балка изогнется еще больше и прогиб б каждом сечении увеличится на величину y1. Полный прогиб ее в любом сечении
у = у0 + у1
Величина полного прогиба будет плечом для сжимающей силы Р, следовательно, в каждом сечении балки помимо момента М0 от действия поперечной нагрузки появится момент Мг от силы Р:
М1=Ру=Р(у0+у1).(1)
Обозначим кривизну балки от действия поперечной нагрузки через 1/r0. Так как сжимающая сила увеличивает изгиб балки, то общая кривизна балки от действия поперечной нагрузки и сжимающей силы Р будет 1/r. Значит, приращение кривизны, вызываемое сжимающей силой Р, составит
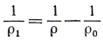 . (2)
. (2)
Так как приращение кривизны вызвано изгибающим моментом М1, то кривизна 1/r1 и изгибающий момент М1 оказываются связанными соотношением
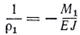 . (3)
. (3)
Выразим приращение кривизны через вторую производную от приращения прогиба у1:
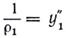 .
.
Подставив кривизну 1/r0 и изгибающий момент М1 в формулу (3), получим
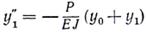 .
.
Перенесем неизвестные в этом уравнении в левую часть и, обозначив k2=P/EJ, запишем дифференциальное уравнение продольно-поперечного изгиба:
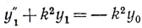 . (4)
. (4)
Это уравнение полностью совпадает с уравнением, записанным для стержня, имеющего небольшое начальное искривление. Правая часть его у0=у0 (х) представляет собой изогнутую ось балки от действия поперечной нагрузки.
Таким образом, составлению дифференциального уравнения продольно-поперечного изгиба должен предшествовать расчет, в результате которого находится изогнутая ось балки от действия поперечной нагрузки.
Предположим, что изогнутая ось балки найдена. Тогда, подставляя выражение у0=у0 (х) в правую часть уравнения (4) и производя интегрирование, найдем приращение прогибов у1 и изгибающих моментов М1 в любом сечении балки от действия сжимающей силы. Складывая изгибающий момент М1 от силы Р сизгибающим моментом М0 от поперечной нагрузки, найдем полный изгибающий момент в любом сечении стержня.
Решение задачи можно значительно упростить, если представить изогнутую ось балки от поперечной нагрузки в силу ее пологости в виде полуволны синусоиды со стрелой, равной максимальному прогибу балки:
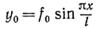 .
.
Предположим также, что дополнительные прогибы у в каждом сечении балки от действия сжимающей силы Р распределяются по закону синуса:
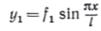 .
.
Подставляя принятые приближенные решения в уравнение (4), получим
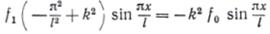 .
.
Отсюда найдем стрелу прогиба f1:
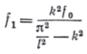 .
.
Это решение полностью совпадает с решением задачи о стержне, имеющем небольшое начальное искривление. Поэтому запишем сразу окончательную формулу для вычисления полного прогиба в середине стержня:
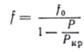 . (5)
. (5)
Изгибающий момент в любом сечении стержня от действия сжимающей силы Р определим по формуле
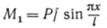 .
.
Проверка стержня на прочность производится по наибольшему изгибающему моменту. Для этого сначала найдем наибольший изгибающий момент М0 от действия поперечной нагрузки и определим сечение, в котором действует этот момент. Пусть это сечение будет х=с. Затем определим изгибающий момент М1 в этом сечении от действия сжимающей силы Р:
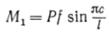 .
.
Складывая эти моменты, найдем полный изгибающий момент в этом сечении
М = М0+М1.
При проверке на прочность нужно потребовать, чтобы напряжения в крайних волокнах наиболее опасного сечения не превышали допускаемых:
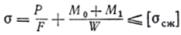 .
.
Пример 1:Балка длиной l=4 м загружена в середине пролета вертикальной силой Р=10 кн и сжимается центрально приложенной силой P1=150 кн (рис. 2). Подобрать сечение в виде двутавра, материал — Ст. 3.
Решение: Сначала подберем сечение из условия поперечного изгиба. Максимальный изгибающий момент в середине пролета
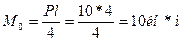
Определим требуемый момент сопротивления:
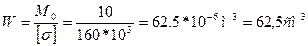
По сортаменту нужно принять двутавр № 36. Однако, учитывая неблагоприятное влияние сжимающей силы, примем сечение с некоторым запасом: двутавр № 40, .F=71,4 см2, Jу=666 см4, Wу==85,9 см3, iy=3.05 см.
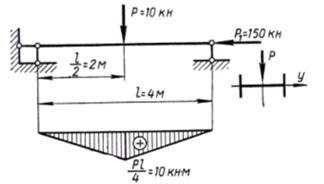
Рис.2.
Проверим подобранное сечение на устойчивость в плоскости наименьшей жесткости. Гибкость стержня
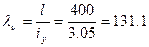
Выпишем значения коэффициентов j:
при l=130 j= 0,40;
при l= 140 j=0,35.
Вычислим значение j для Х= 131,1:
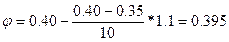
Допускаемая сжимающая сила
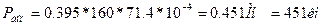
Так как сжимающая сила принята Р1=150 кн, то устойчивость стержня обеспечена.
Проверим теперь фактические напряжения в крайних волокнах наиболее опасного сечения. Максимальный прогиб в середине стержня от поперечной нагрузки
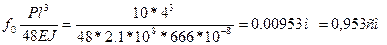
Для того чтобы вычислить полный прогиб, найдем сначала величину критической силы
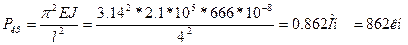
Полный прогиб в середине стержня
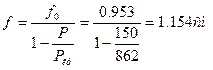
Вычислим дополнительный изгибающий момент от действия сжимающей силы:
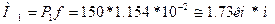
Полный наибольший изгибающий момент и в середине стержня
М = М0 + М1=10+1,73=11,73 кн*м.
Определим наибольшие сжимающие напряжения:
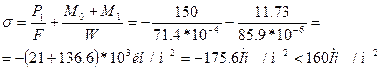
Подобранное сечение удовлетворяет условию прочности.
Дата добавления: 2015-08-01; просмотров: 2373;
