Лекция 22. Расчет изгибаемых балок с тонкостенным поперечным сечением
Расчет изгибаемых балок с тонкостенным поперечным сечением
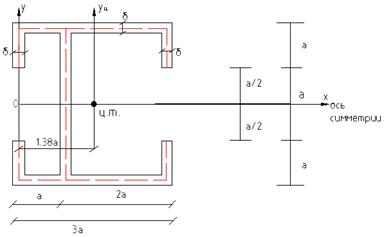
Тонкостенностью называются поперечные сечения, у которых 
а- длина элемента профиля
δ- толщина элемента профиля
Для тонкостенных поперечных сечений дополнительно возникает напряжение:
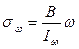 (1)
(1)
Причем 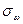 вносит существенный вклад в общее напряженное состояние.
вносит существенный вклад в общее напряженное состояние.
Сначала необходимо определить все геометрические характеристики поперечных сечений
1) Определение положения центральной точки поперечного сечения:
выбираем произвольную ось OY
Координаты центральной точки определить по формуле:
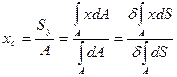
Подсчитаем статические моменты площади и площади поперечного сечения:
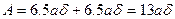 - при этом все размеры берутся в осях элемента.
- при этом все размеры берутся в осях элемента.
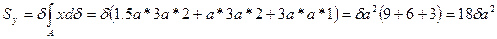
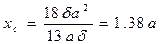 - решение между осью у и центральной точкой сечения.
- решение между осью у и центральной точкой сечения.
2) Определяем величины Моментов инерции сечения относительно оси Xc и Yc
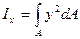
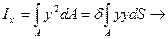 по формуле Симпсона.
по формуле Симпсона.
Можно построить эпюру у:
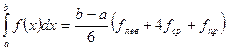 - формула Симпсона
- формула Симпсона
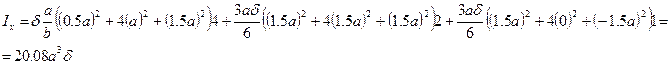
Аналогично может быть подсчитана величина Iy:
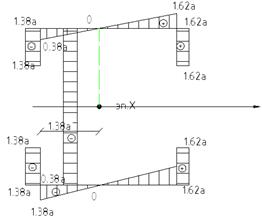
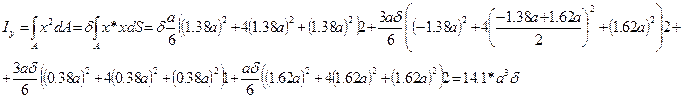 Если использовать для подсчета геометрических характеристик точное выражение, то получаем:
Если использовать для подсчета геометрических характеристик точное выражение, то получаем:
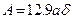 . Погрешность в вычислениях:
. Погрешность в вычислениях: 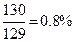
Статический момент площади: 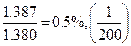
Координаты центра точек:
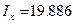 , погрешность
, погрешность 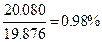
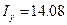 ,
, 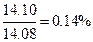
Итак, выполненные приближенные вычисления обладают высокой точностью.
В формуле для моментных напряжений:
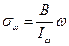
Определение: секториальной площадью 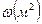 называется величина, равная удвоенной площади треугольников, описывающих при движении точки по оси элементы сечения.
называется величина, равная удвоенной площади треугольников, описывающих при движении точки по оси элементы сечения.
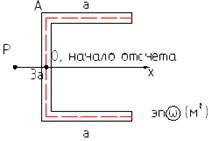

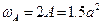
Правило №1: в местах соединения элементов профиля 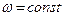
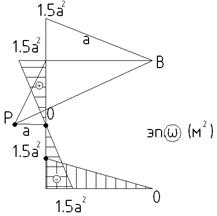
Правило №2: при движении конца вектора по прямой, 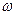 меняется по закону прямой линии.
меняется по закону прямой линии.
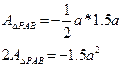
При определенном выборе положения полюс эпюра 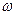 получается в простейшем полюсе.
получается в простейшем полюсе.
Правило №3: если при движении вектора по прямой треугольники получается вырожденными, то площадь 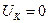
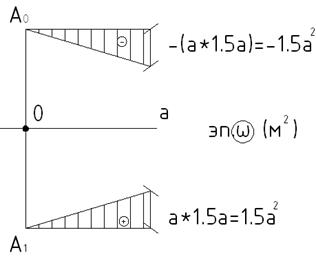
Для дальнейших вычислений стремимся к наибольшей простой эпюре 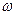 .
.
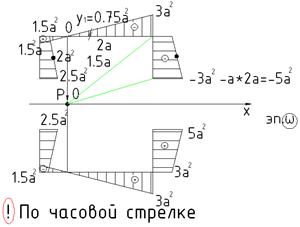
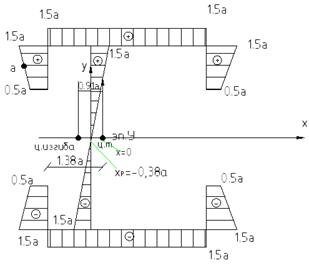
Понятие о центре изгиба:
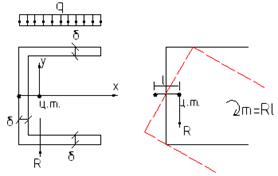
Если равнодействующая, приложенная к нагрузке R, проходящая через центр точки сечения, то создается момент, равный произведению R на решение между центром точки и центром изгиба.
В результате поперечное сечение будет закручиваться вокруг центра изгиба, в данном случае по часовой стрелке.
Если равнодействующая R действующая в точке изгиба, то сечение деформируется без закручивания и напряжение можно подсчитать по формуле: 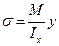
В реальном случае: 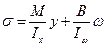 , причем второе слагаемое вносит существенный вклад в напряженное состояние.
, причем второе слагаемое вносит существенный вклад в напряженное состояние.

Для получения центра изгиба используется формула:
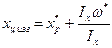 (2)
(2)
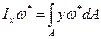 - центробежный секториальный момент относительно оси Х.
- центробежный секториальный момент относительно оси Х.
Тогда 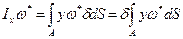
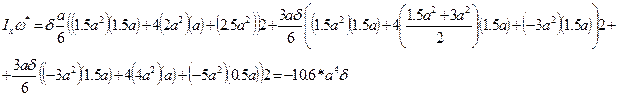
Тогда координата центра изгиба получается по формуле:
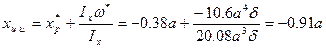 : в главных центральных осях (Iц) необходимо отстроить по оси ОХ на 0,91.
: в главных центральных осях (Iц) необходимо отстроить по оси ОХ на 0,91.
Для дальнейших вычислений потребуется эпюра 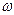 , взятая для полюса в центре изгиба:
, взятая для полюса в центре изгиба:
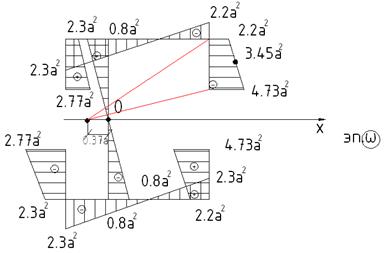
В формулу напряжения входит секториальная величина для ω:
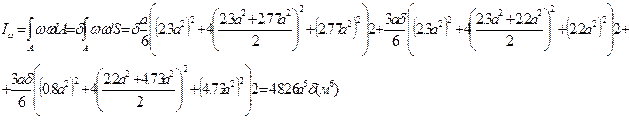
Дата добавления: 2015-08-01; просмотров: 1263;
