Лекция 23
Расчет изгибаемых балок с тонкостенным поперечным сечением
на стестенное кручение
При обычном изгибе балки используется функция у(м)- прогиб
у(м) –прогиб 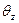 - участок закручивания (рад)
- участок закручивания (рад)
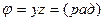 - угол поворота
- угол поворота 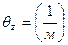 - искривление поперечного сечения стержня)
- искривление поперечного сечения стержня)
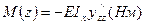 - изгибающий момент
- изгибающий момент 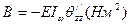 - бимомент
- бимомент
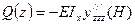
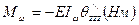 - изгибный момент
- изгибный момент
При кручении тонкостенного профиля возникает крутящий момент:
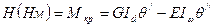 (1) - составляющая крутящего момента
(1) - составляющая крутящего момента
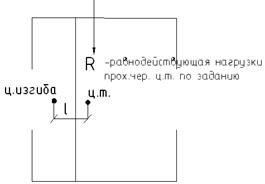
В результате возникает крутящий момент:
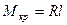
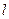 - расстояние от центра изгиба до центра точки
- расстояние от центра изгиба до центра точки
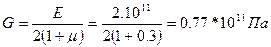
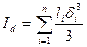
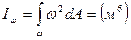 - секториальный момент площади при
- секториальный момент площади при 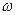 полюсе в центре изгиба.
полюсе в центре изгиба.
Приводим уравнение (1) к виду:
Дифференцируем уравнение (1): 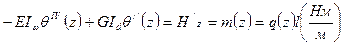 - погонное колебание
- погонное колебание
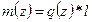
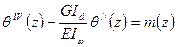 (2)
(2)
Вводим обозначения: 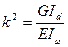 ;
; 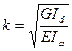 (3)
(3)
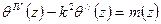 - может быть решено методом начальных параметров в соответствии с граничными условиями по концам балки.
- может быть решено методом начальных параметров в соответствии с граничными условиями по концам балки.

Два начальных параметра определяются сразу из условий на левом конце балки, другой начальный параметр подсчитывается из системы уравнений, записанных для правого конца балки.
Нагрузка занимает всю балку целиком.
Тогда по методу начальных параметров выражения для функций будут иметь вид:
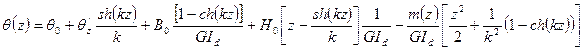
Все остальные функции получаются дифференцированием приведенного выражения
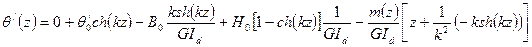
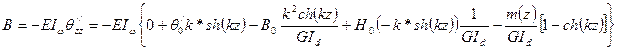
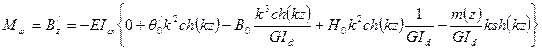
Рассматриваем вновь следующее поперечное сечение:
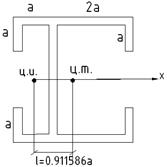
Ранее были подсчитаны следующие геометрические характеристики
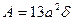 ,
, 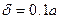 ,
, 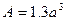 ,
, 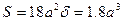 ,
, 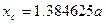
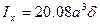 ,
, 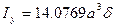 ,
, 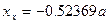 ,
, 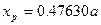 ,
,
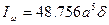
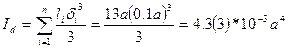 ,
, 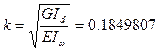
Принимая 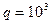 (Н/м);
(Н/м); 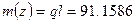 (Нм/м)
(Нм/м)
Для трех схем:
1й случай:
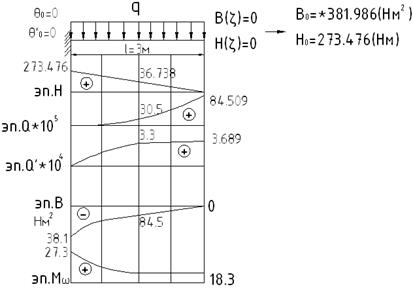
Угол закручивания зависит от k.
2й случай:
Эпюра получается разворотом предыдущей эпюры при частичной смене знаков.
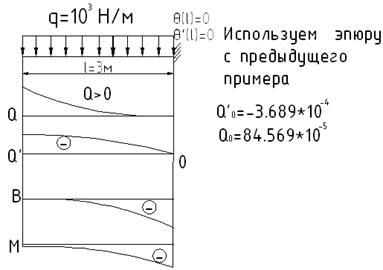
3й случай:
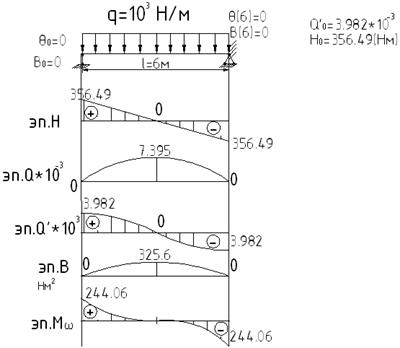
Затем необходимо построить следующие эпюры нормальных напряжений в поперечном сечении балки:
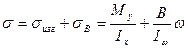
Сечения, где действуют 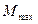 и
и 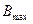 для всех типов закрепления балок совпадает, т.е. возможно рассмотреть следующие сечения:
для всех типов закрепления балок совпадает, т.е. возможно рассмотреть следующие сечения:

Показываем характерный вид составленных эпюр у
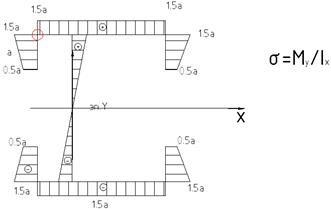
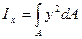
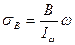
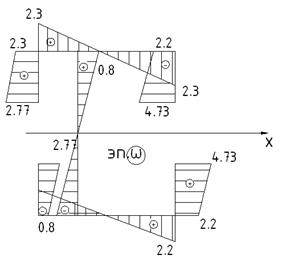
В качестве точки, где выбрана 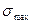 берем точку О
берем точку О
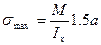
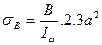
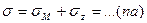
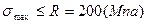
При 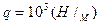
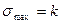
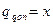
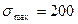
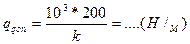
Дата добавления: 2015-08-01; просмотров: 793;
