Теорема о скоростях точек плоской фигуры

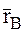Пусть плоская фигура движется в своей плоскости (рис. 5), в которой положение произвольной точки В и полюса D определяются соответственно радиус-векторами и .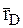

Тогда в любой момент времени

. (7.1)

Возьмем производную по времени от выражения (7.1):

.

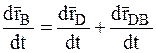Рис. 5

Так как (DВ=const) изменяется при движении плоской фигуры только за счет изменения направления (поворота), то на основании (1.21) получим:

,

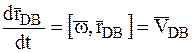здесь — скорость точки плоской фигуры вследствие вращательного движения плоской фигуры относительно полюса D. Кроме того, 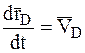, а , следовательно:

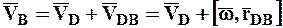. (7.2)

Теорема: Скорость точки плоской фигуры равняется геометрической сумме скорости точки, выбранной в качестве полюса, и скорости этой точки вследствие вращательного движения плоской фигуры относительно полюса (рис. 6).

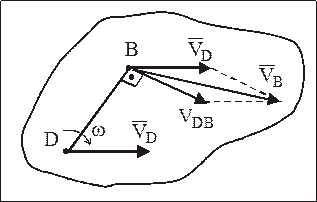
Рис. 6