Три задачи по расчету простого трубопровода

Все основные расчеты, связанные с простым трубопроводом сводятся к решению следующих трех задач.

Задача 1. Заданы:Расход Q, диаметр d и длина l трубопровода, все величины местных сопротивлений z_i, эквивалентная шероховатость материала стенок трубопровода к_э, кинематический коэффициент вязкости жидкости n.

Определить:Напор H.

Имея заданные величины, их подставляют в основную зависимость (2.7) и находят Н. Так что первая задача решается простым вычислением; она является основной, так как к ней сводится решение остальных двух. Типичный пример первой задачи – определение высоты водонапорной башни для создания заданного режима.

Задача 3.1 Найти напор Н (например высоту Н водонапорной башни), если от нее по трубе диаметром d=50мм и длиной l=75м необходимо передать расход воды Q=3,5л/с. Трубы новые, стальные, К_Э=0,06мм, сумма всех коэффициентов местных сопротивлений равна 3,8, т.е. Σξ=3,8.

Решение. Находим число Рейнольдса Re по формуле:

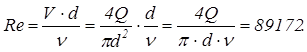
Затем находим значение параметра (Re·К_Э)/d=107 для установления зоны сопротивления. Зона сопротивления – доквадратичная, поэтому применяем формулу А. Д. Альтшуля 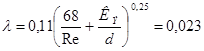. Окончательно подставляем данные в формулу

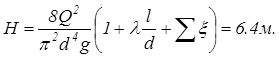
Таким образом искомое значение напора равно 6,4метра.

Задача 2. Заданы:Напор H, диаметр d и длина l трубопровода, все величины z_i, к_э и n.

Определить: Расход Q.

Ошибочной в данном случае может показаться простота решения уравнения (2.7) путем извлечения квадратного корня. На самом деле во всех зонах, кроме квадратичной, величина l зависит от числа Rе

,

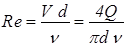а, следовательно, от расхода Q. Если подойти формально к решению второй задачи, то (2.7) представляет уравнение с одним неизвестным, которое решается по известным алгоритмам с помощью ЭВМ. В инженерной практике может быть полезен прием решения (2.7) называемый графоаналитическим способом. Если задаться несколькими (5 - 10) произвольными, но реальными числовыми значениями расхода Q и подставить их в (2.7), то получится столько же числовых значений Н. Затем в системе координат Q – H наносят эти точки и соединяют их плавной кривой; она, как видно из (2.7) представляет квадратичную параболу, симметричную относительно оси H, рис. 3.1., (имеет смысл ее ветвь при Q > 0).

Построенная по точкам, она отражает зависимость Q от H только для данного трубопровода, поэтому из графика по известному значению Н находят искомое значение Q.

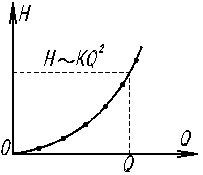
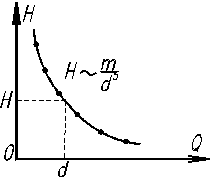
Рис. 3.1. Рис. 3.2.

Необходимо задавать такие величины расходов, чтобы получать напоры как меньшие, так и большие заданного.

Задача 3.2 Определить величину расхода Q, проходящему по трубопроводу диаметром d=50мм и длиной l=115м, если разность уровней в начале и в конце трубопровода равна Н=4,3м. Трубы стальные, К_Э=0,05мм, сумма всех коэффициентов местных сопротивлений равна 3,2, т.е. Σξ=3,2.

Решение. В данном случае имеем одно уравнение (2,7) и одну неизвестную величину – расход Q, поэтому задачу лучше всего решать на ЭВМ одним из известных приближенных методов. Для инженерных расчетов применим простейший метод подбора. В качестве первоначального задаем расход, равный Q₁=2,5л/с. Посмотрим теперь, какому значению напора Н соответствует заданное значение Q₁=2,5л/с, т. е. решаем первую задачу по расчету простого трубопровода. Находим последовательно: Re₁=63694, (Re₁·К_Э)/d=64, λ₁=0,023, Н₁=4,8м. Получен напор, больший заданного, поэтому необходимо взять меньший расход, например Q₂=2,2л/с, при этом расходе: Re₂=56051, (Re₂·К_Э)/d=56, λ₂=0,024, Н₂=3,8м. Ясно, что искомый расход заключен между Q₁ и Q₂ и любой расход, взятый из этого промежутка сужает интервал поиска. Продолжая задание расходов из интервала Q₁ > Q_X > Q₂ и сравнивая полученные значения Н_Х с заданным Н=4,3м, возможно решить задачу с любой точностью.

Если в данном случае применить формулу

,

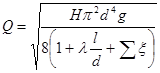то получим (определяя λ как в квадратичной зоне) Q=2,57л/с, что является завышенным по сравнению с действительным значением.

Задача 3. Заданы:Напор Н, расход Q, длина трубопровода, все величины z_i, к_э и n.

Определить:Диаметр d.

В этом случае уравнение (2.7) невозможно решить аналитически, но формально – это уравнение с одним неизвестным и решение его на ЭВМ трудностей не представляет. Для инженерных расчетов удобно применить графо-аналитический способ. Кривая зависимости H от d является гиперболой; как это следует из (2.7): при d → 0, H → ∞. При d → ∞, H → 0, рис. 3.2.

Для решения задач задают несколько значений диаметров, строят кривую и по известному значению Н находят искомое значение d.

Задача 3.3. Определить диаметр трубопровода, который должен пропускать расход Q=5,6л/с при действуюшем напоре Н=3,0м. Длина трубопровода l=80м, К_Э=0,05мм, сумма коэффициентов местных сопротивлений на трубопроводе Σξ=4,5.

Задача 3.4.При каких условиях решение задачи 2 (определение расхода) может быть получено в виде

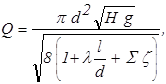
т.е. аналитически.

Решение.Выражение, приведенное в условии задачи может быть получено в квадратичной области сопротивления, т.е. когда коэффициент гидравлического сопротивления l не зависит от числа Рейнольдса, а следовательно и от расхода. В этом случае точной является часто используемая при решении задач зависимость

Н = K × Q²,

где К – постоянная, на зависящая от Q.

Задача 3.5.Представим, что на дачном участке находится емкость с водой для полива, из которой выходит через отверстие отрезок шланга. Пояснить будет ли изменяться расход, а если будет, то как и по каким причинам, если: а) увеличить длину шланга; б) уменьшить диаметр шланга; в) немного прикрыть кран, ранее полностью открытый; г) изогнуть шланг (устроить поворот); д) увеличить диаметр шланга.

4. Последовательное и параллельное

соединение простых трубопроводов

Последовательное соединение

Рассмотрим систему из последовательно соединенных труб различных диаметров и длин. Такое соединение участков трубопровода называется последовательным,рис. 4.1.

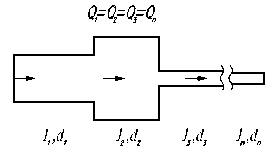
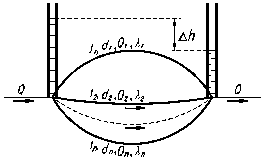
Рис.4.1. Рис.4.2.

H = H₁ + H₂ + H₃ + …+ H_n,

где H₁, H₂ , H₃, …, H_n – потери напора на 1, 2, 3, …n-ом участке.

Учитывая, что для каждого участка последовательного соединения справедлива зависимость (2.7) и имея в виду, что на каждом участке расход одинаковый, запишем (4.2) в виде:

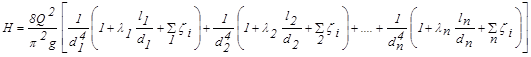Из (4.3) следует, что решение первой и второй задач при последовательном соединении участков трубопровода разного диаметра будет таким же как для простого трубопровода (трубопровода постоянного диаметра).

Третья же задача, если в ней потребовать определения диаметров для всех участков, становится неопределенной, так как в этом случае уравнение (4.3) содержит n неизвестных. Для решения этой задачи необходимо задать диаметры труб для всех участков, кроме одного, который может быть тогда определен.

Задача 4.1. Определить потери напора в стальном трубопроводе, состоящем из двух участков длиной l₁ = 120 м и l₂ = 250 м. Диаметры труб участков d₁ = 120 мм и d₂ = 100 мм. Расход воды в трубопроводе Q = 12,2 л/с, кинематический коэффициент вязкости воды принять равным n = 0,01 см²/с.

Решение.В данном случае общие потери равны сумме потерь на каждом из участков. По справочнику определяем к_Э = 0,02 мм.

Определяем последовательно для первого участка

V₁ = 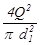= 1,1 м/с; Re₁ = 129511; Re₁× 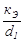= 10,7; l₁ = 0,017;

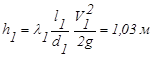
Аналогично для второго участка

V₂ = 1,55 м/с; Re₂ = 155414; Re₂ = 31; l₂ = 0,017;

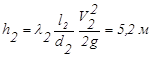; h₁ + h₂ = 6.23 м.

Ответ:общие потери напора равны 6,23 м.