Тупиковые и кольцевые водопроводные сети
На рис. 5.1 приведен пример разветвленной (тупиковой) водопроводной сети; из него видно, что каждый участок может быть представлен как простой трубопровод. Участки заканчиваются водоразборными устройствами, т.е. эти точки являются для потока «тупиками» (откуда и название сети).
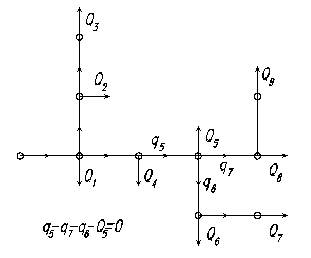
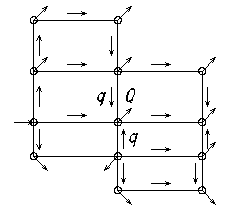
Рис. 5.1. Рис. 5.2.
В большинстве случаев при расчете такой сети расходы в точках водоразбора задаются (они обусловлены нуждами потребителей) и требуется определить напор в начальной точке.
Такой вариант расчета встречается при установке в этой точке насоса, который подбирается на требующийся по гидравлическому расчету напор или для определения высоты водонапорной башни. Для такого типа сети на каждом участке расход может быть определен однозначно и при расчете вначале выбирают наиболее удаленную, «критическую» точку и от нее начинают считать потери.
|
H = Hсв + (zN - zH) + å hW,
где Н – требуемый напор в начале трубопровода, N – номер водоразборной точки в конце последнего участка, (vzN - zH) – разность отметок N-ой водоразборной точки и начальной точки водопровода, å hW – сумма потерь напора в данном направлении, считая от первого до последнего участка включительно.
Уравнение (5.1) можно сформулировать так: требуемый напор для сети равен сумме потерь напора от начальной его точки до самой невыгодной в гидравлическом отношении точки водоразбора N плюс свободный напор в точке N плюс разность геометрических (геодезических) отметок точки N и начальной точки (необходимость учёта zN и Hсв очевидна, так как самая удалённая точка водоразбора может находиться на значительной по сравнению с zN высоте, а также может возникнуть необходимость развить в этой точке большое давление, - т.е. большое значение Hсв). . Для каждого узла всегда должно выполняться равенство, следующее из уравнения неразрывности – сумма приходящих расходов к узлу должна быть равна сумме уходящих от него; это обычно записывается в виде «узлового» уравнения
|
При этом расходы, приходящие к узлу условно считают положительными, а уходящие от узла (включая отбор) – отрицательными.
Расчет водопроводной сети обычно состоит в нахождении диаметров труб, а потери на любом участке при заданном расходе могут иметь разные значения в зависимости от его диаметра (теоретически труба любого диаметра пропустит любой расход; при этом будут разные скорости и разные потери напора).
При увеличении диаметра потери уменьшаются и поэтому уменьшается требуемая мощность насоса; одновременно с увеличением диаметра возрастает стоимость как самих труб так и стоимость их прокладки. Поэтому с учетом всех гидравлических и экономических факторов вводится понятие экономически наивыгоднейшего диаметра; само его значение в зависимости от расхода определяется по специальным таблицам.
На рис. 5.2 приведена схема водопроводной сети, получившая широкое распространение; она называется замкнутой или кольцевойсетью. Общая длина трубопроводов кольцевой сети больше, чем у тупиковой; соответственно и стоимость кольцевой сети больше. В некоторую точку (пункт) с помощью тупиковой сети вода может быть подана единственным путем, а в кольцевой в ту же точку может быть подана разными путями; в этом состоит одно из главных преимуществ кольцевой сети – ее высокая надежность и бесперебойная работа во время аварии на каком-либо участке. Расчет кольцевой сети представляет собой сложную задачу, которая сводится к решению большого числа уравнений. Необходимо заметить, что и в кольцевой сети в любом узле выполняются «узловые» уравнения (5.2).
Задача 5.1.Есть простейшая тупиковая сеть, рис.5.3 и полученная из нее путем добавления участка 2-4 кольцевая сеть (одно кольцо), рис. 5.4.
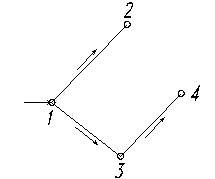
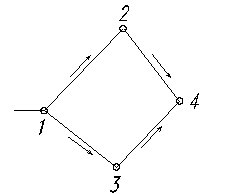
Рис. 5.3 Рис. 5.4
Подсчитать и сравнить вероятности бесперебойной подачи воды в пункт 4 в обоих случаях. В качестве функции описывающей вероятность бесперебойной работы отдельного участка в течении времени t принять функцию P = e-l t, где l - интенсивность отказов (показательный закон надежности).
Решение.Для функции P: а) Р = 1 при t = 0, б) при увеличении t значение Р уменьшается, в) при умножении Р1, Р2, …Рn = e 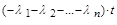 , и это произведение меньше любого из сомножителей. Допустим, что для участка 1–2 – P1-2 = e
, и это произведение меньше любого из сомножителей. Допустим, что для участка 1–2 – P1-2 = e 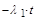 , аналогично P1-3 = e
, аналогично P1-3 = e 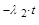 , P3-4 = e
, P3-4 = e 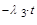 , P2-4 = e
, P2-4 = e 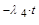 . Когда имеем тупиковую сеть, то искомая вероятность равна
. Когда имеем тупиковую сеть, то искомая вероятность равна
P4Т = e 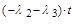
(по формуле умножения вероятностей). В случае кольцевой сети вероятности безотказной работы частей 1-2, 2-4 и 1-3, 3-4 независимы и искомая вероятность равна
P4К = e 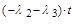 + e
+ e 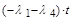 - e
- e 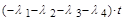 ,
,
откуда следует, что P4К > P4Т.
Дата добавления: 2015-08-01; просмотров: 6209;
