Уравнение для расчета простого трубопровода

Простой трубопровод – это труба постоянного диаметра с местными сопротивлениями, по которой проходит постоянный расход.

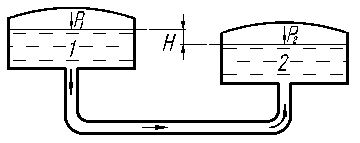
Большинство простых трубопроводов вписывается в одну из следующих двух схем, рис. 2.1.; в резервуарах уровень поддерживается постоянным и поэтому течение везде установившееся.

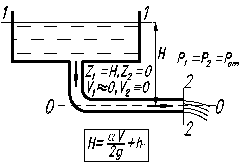
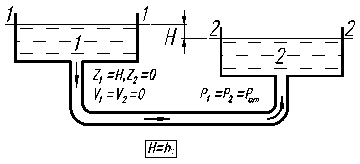
Схема 1 Схема 2

Рис.2. 1.

В обоих случаях движущей силой является сила тяжести, которая приводит к разности давлений и под действием этой разности жидкость приходит в движение. В обоих случаях потенциальная энергия положения преобразуется в кинетическую энергию, а последняя – в тепловую за счет сил трения.

.

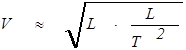Точнее результат для скорости течения получается, если приравнять запас потенциальной энергии и кинетическую энергию текущей жидкости.

Для случая идеальной жидкости

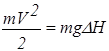или .

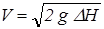В действительности вследствие вязкости (трение в жидкости) часть кинетической энергии переходит в тепловую. Поэтому чем больше сопротивлений по длине и местных, тем скорость течения меньше.

Как это часто бывает, наиболее точный и исчерпывающий результат получается при решении общих уравнений. В данном случае вполне понятно, что основным уравнением, связывающим запас потенциальной энергии, кинетическую энергию потока и потери является уравнение Бернулли

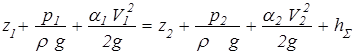
Суммарные потери h_Σ складываются из потерь по длине h_l и местных h_м

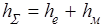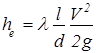
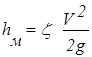Выбираем плоскость (ось) сравнения, совпадающей с осью горизонтальной части трубопровода, а сечения 1-1 и 2-2 совпадающими со свободными поверхностями в сосудах, рис. 2.1.

Физический смысл уравнения для схемы 1 следующий: потенциальная энергия положения частично преобразуется в кинетическую энергию жидкости, вытекающей в атмосферу и частично превращается в тепло. Для схемы 2 имеем H=h_пот, т.е. вся потенциальная энергия полностью преобразуется в тепло.

Уравнения баланса энергии для обеих схем имеют одинаковый вид, а именно

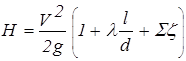
В случае схемы 2 из всей суммы коэффициентов местных сопротивлений выделяется коэффициент внезапного расширения при входе трубы в емкость 2 (он равен единице, т.е. z = 1).

Если труба круглая, то (2.6) преобразуется к виду (V = 4Q/pd²)

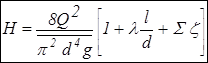
Это уравнение будем в дальнейшем называть уравнением для расчета простого трубопровода.

Задача 2.1. Вывести уравнение для расчета простого трубопровода при перетекании жидкости из одного закрытого резервуара в другой под действием силы тяжести и давления газа на поверхностях. Рассмотреть случаи:

а) перетекание из 1 в 2; б) перетекание из 2 в 1; в) жидкость покоится. Написать условия перетекания и сделать краткий анализ решения.