Распределение нагрузки между турбоагрегатами ТЭС
Для ТЭС по характеристикам турбоагрегатов (ТА) составляются характеристики относительных приростов (ХОП) расходов теплоты, энергетические характеристики машинного зала электростанции и режимные карты. Характеристика относительных приростов и энергетическая для электростанции в целом могут быть
получены на основе одноименных характеристик котельной и машинного зала.
Относительный прирост (ОП) расхода топлива станцией является показателем экономичности работы станции или блока и показывает, на сколько изменится расход топлива станцией при изменении нагрузки на 1 кВт:
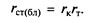
Скачок на ХОП электростанции (рис. 13.2, а) связан с ХОП турбоагрегата (рис. 13.12, б), а пологовогнутая часть определяется ХОП котла (рис. 13.12, в). Если в машинном зале станции установлены однотипные агрегаты, то нагрузка между ними распределяется равномерно при минимально необходимом числе агрегатов, что позволяет дать каждому агрегату достаточно высокую нагрузку. Если агрегаты разнотипны по мощности и экономичности, то должно быть произведено экономичное распределение электрической нагрузки между ними, т. е. заданная электрическая нагрузка распределяется между ними таким образом, чтобы в машинном зале расход тепла был минимальным.
Рассмотрим простейший пример. В турбинном цехе установлены два агрегата различного типа. При этом возможны два основных случая.
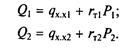
|
| 1. Если qxx1 < gxx2 и гт1 < гт2, то любая нагрузка ТЭС должна покрываться турбиной № 1 (рис. 13.13, а). |
I. Нагрузка ТЭС может быть покрыта полностью каждым из двух агрегатов. Их расходные характеристики определяются следующим образом:
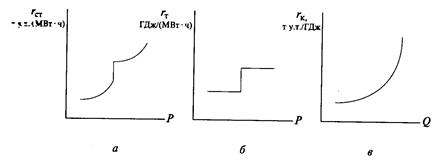
Рис, 13.12. Построение характеристики относительных приростов расхода
топлива тепловой электростанцией: а — электростанции; б — турбоагрегата; в — котла
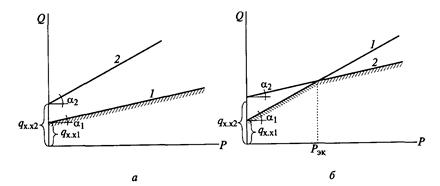
Рис. 13.13. Полное покрытие нагрузки ТЭС одним из агрегатов:
а — нагрузка ТЭС полностью покрывается турбиной № 1; 6 — в зоне Р < Рж
нагрузка ТЭС полностью покрывается турбиной № 1, в зоне Р>РЖ — полностью
турбиной № 2; 1, 2 — расходные характеристики турбин
2. Если qxx1 < qxx2,, rT1 > rT2,, 0<Р< Pmax (рис. 13.13, б), то в диапазоне Р< Рэк Qmin= Q2, следовательно, надо загружать турбину № 1; в диапазоне Р>РЖ (Ln = Q2, следовательно, надо разгружать турбину № 1 и загружать турбину № 2; при Р = Рж турбины равно-экономичны.
Если сходящиеся характеристики не пересекаются в зоне номинальной мощности, то всю нагрузку должна взять на себя турбина № 1.
11. Нагрузка ТЭС может быть покрыта только при совместной параллельной работе обоих агрегатов.
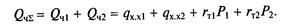
|
| Прибавим и вычтем произведение гт1Р2, а общую нагрузку двух агрегатов обозначим через Рст= Р1 + Р2. Тогда |
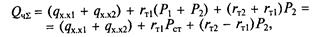
|
Допустим, что совместно работают два турбоагрегата, из которых первый имеет часовую расходную характеристику Qч1 = qxx1 + rT1Р1, а второй Qч2 = qxx2 + rT1Р2. Общий часовой расход тепла двух совместно работающих агрегатов составит
и графическое изображение расходной характеристики этих двух совместно работающих агрегатов будет иметь вид ломаной линии, точка излома которой может перемещаться при перераспределении нагрузки между агрегатами. Как видно из выражения общего расхода тепла, при любом распределении нагрузки между агрегатами суммарный расход тепла на холостой ход останется неизменным (qxxl + qxx2), а переменная часть расхода тепла будет тем
меньше, чем больше нагружается агрегат, имеющий меньший относительный прирост расхода тепла.
Итак, в системе параллельно работающих агрегатов экономичность вариантов распределения нагрузки изменяется только за счет изменения дополнительного расхода энергии, так как расходы на холостой ход агрегатов имеют место при любом распределении нагрузки между ними. Следовательно, при возрастании нагрузки совместно работающих агрегатов в первую очередь должен нагружаться тот из них, у которого меньше относительный прирост расхода первичной энергии. Таким образом, оптимальное распределение достигается в порядке возрастания относительных приростов расходов тепла: rт1 < rт2 < rTi.
Режимная карта машинного зала тепловой станции — это зависимость электрической нагрузки отдельных турбоагрегатов от электрической нагрузки станции: Рi =f(Р). Режимная карта разрабатывается на основе ХОП определенного состава работающих турбоагрегатов применительно к данным тепловым нагрузкам и условиям эксплуатации и используется для оптимального распределения суммарной нагрузки ТЭС между ними.
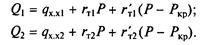
|
| Допустим, что относительные приросты расхода тепла по зонам нагрузки находятся в следующем соотношении (рис. 13.14): |
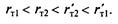
|
Допустим, что совместно работают два агрегата со следующими энергетическими характеристиками:
Технические минимумы нагрузки обозначим соответственно Pmin1 и Pmin2. Тогда может быть построена режимная карта экономического распределения нагрузки между этими агрегатами при их совместной работе.
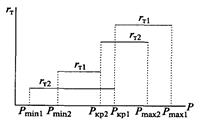
|
| Рис. 13.14. Относительные приросты расхода тепла турбоагрегатами по зонам нагрузки |
По оси абсцисс (рис. 13.15) отложена общая нагрузка агрегатов станции (т. е. нагрузка турбинного цеха), а по оси ординат — нагрузка каждого из совместно работающих агрегатов. В первую очередь на график наносится технический минимум нагрузки цеха Рст min= Pmin1 + Pmin1 Далее с увеличением нагрузки цеха догрузка .агрегатов производится в последовательности возрастания относительных приростов (табл. 13.1).

|
ку электрическая нагрузка, вырабатываемая по теплофикационному режиму, определяется тепловыми нагрузками. Распределение тепловых нагрузок ТЭЦ производится в последовательности убывания удельной выработки электроэнергии на тепловом потреблении, т.е. соблюдается принцип максимальной выработки электроэнергии на тепловом потреблении.
Поэтому для ТЭЦ распределение электрических нагрузок между турбинами заключается в определении целесообразной дополнительной нагрузки конденсационной мощности, которая может меняться:
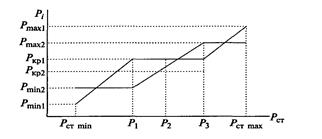
Рис. 13.15. Режимная карта машинного зала тепловой станции
Сначала догружается агрегат № 1 до нагрузки Ркр1, за пределами которой относительный прирост возрастает. На графике это отображается наклонным к оси абсцисс отрезком прямой, показывающим, как с ростом нагрузки цеха увеличивается нагрузка агрегата № 1, в то время как нагрузка агрегата № 2 остается постоянной — на уровне технического минимума. Таким образом, в покрытии нагрузки цеха Р1 агрегат № 1 участвует величиной РкрЬ а агрегат № 2 — величиной Рmin2
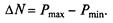
Распределение этой конденсационной мощности производится аналогично КЭС, т.е. в порядке возрастания относительных приростов. Если условие параллельной работы не соблюдается и турбины ТЭС включаются последовательно по мере нагрузки станами, то при распределении нагрузки между ними надо учитывать не только величину относительного прироста, но и расход тепла на холостой ход.

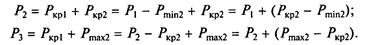
|
| В последнюю очередь догружается агрегат № 1 в зоне |
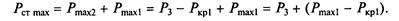
|
Далее возрастающая нагрузка цеха передается на агрегат № 2 (так как rт2 < r'т2 < r'т1), который нагружается сначала до величины Р2, а затем до Р3, в то же время нагрузка агрегата № 1 остается на уровне Ркр1:
Распределение электрической нагрузки ТЭЦ зависит от того, как распределены между турбинами тепловые нагрузки, посколь-
Таблица 13.1 Зависимость зоны нагрузки от относительных приростов
| Значение ОП | №ТА | Зона нагрузки |
| rт1 rт2 r'т2 r'т1 | Pmin1-Pкр1 Pmin2-Pкр2 Pкр2-Pmax2 Pкр1-Pmax1 |
Планирование мощности и распределение нагрузки между электростанциями в энергосистеме
Общие вопросы оптимального распределения электрической нагрузки в энергосистеме
В хозяйственном отношении электростанции и электрические сети являются самостоятельными структурными подразделениями, но при выборе режима распределения электрических нагрузок они подчиняются энергосистеме.
Основной целью энергосистемы является бесперебойное снабжение потребителей энергией требуемого качества при условии максимальной экономичности. Нагрузка энергосистемы, заданная ей по плану в соответствии с графиком электрических нагрузок, должна быть распределена между электростанциями таким образом, чтобы достигался максимум экономичности энергосистемы в целом.
Для решения задачи оптимизации с использованием ЭВМ составляется математическая модель, включающая в себя пять уравненийили неравенств.
1. Уравнение цели (критерий экономичности).
Общей целью, или критерием оптимизации режимов, является обеспечение минимальных текущих затрат на производство электроэнергии в энергосистеме
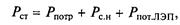
|
| 3. Уравнения ограничения. Они могут быть двух видов: 1) балансовые, в виде равенства: |
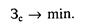
От режима работы электростанции зависят только условно-переменные затраты, к которым относится прежде всего топливная составляющая расходов на ТЭС. Условно-постоянные затраты не зависят от режима работы электростанции и поэтому могут быть исключены из рассмотрения. Целевая функция (критерий оптимизации) может быть представлена следующим выражением:
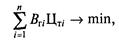
где п — число тепловых станций в энергосистеме; Вгi — годовой расход топлива на i-й станции, т у.т; Цтi — цена топлива, используемого на i-й станции, р./т у.т.
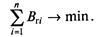
|
| 2. Уравнение связи (или характеристика объекта). Объект представляется в виде следующей модели : |
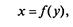
|
Если цены на топливо для станций энергосистемы одинаковы, то целевая функция принимает следующий вид:
где х — первичная энергия, поступающая на объект (входящий поток); у — вторичная энергия (исходящий поток).
Характеристиками объекта являются расходные энергетические характеристики:
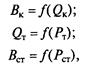
где Вк, Вст — часовой расход топлива соответственно котла и электростанции, т у. т/ч; QK, QT — количество теплоты соответственно на выходе из котла и входе в голову турбины, ГДж/ч; Рт, Рст — электрическая мощность соответственно турбоагрегата и электростанции, МВт.
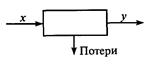
Если характеристика объекта не меняется во времени, то объект называется стационарным, в противном случае — нестационарным. Энергетическое оборудование является типично не-
|
| Рис. 13.16. Модель объекта |
стационарным объектом. В настоящее время нет методики, позволяющей учесть нестационарностъ объекта, поэтому она не принимается во внимание.
где Рст — мощность электростанций, входящих в энергосистему; Рпотр — полезно отпущенная мощность потребителям, МВт; Рсн, Рпот.лэп - потери мощности на собственные нужды и в ЛЭП и подстанциях соответственно;
2) граничные, в виде следующих неравенств, характеризующие технические возможности агрегатов:
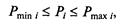
где Рmini и Рmaxi - ограничения по выдаче мощности турбоагрегатами соответственно по минимальному и максимальному значению.
Ограничения бывают жесткие и нежесткие. К жестким относятся граничные неравенства, нарушение которых недопустимо, так как это связано с безопасностью работы установки и угрожает жизни людей. Нарушение нежестких ограничений (баланса мощности в энергосистеме) приводит к нарушению оптимального режима работы, снижению экономичности и дополнительным затратам.
4. Уравнение управления. Оно формируется путем совместного решения первых трех уравнений:

5. Уравнение адаптации. Оно является корректировкой уравнения управления при изменении целевой функции и уравнений связи и характеризует приспособляемость системы к изменяющимся внешним условиям.
Если в рассмотрении присутствуют все пять уравнений, то такая модель называется оптимизационной. При отсутствии в модели уравнения управления она является оценочной. Если анализируется только характеристика объекта, то модель называется моделью для познания. В аварийных ситуациях используется только модель ограничения.
Дата добавления: 2015-08-01; просмотров: 4832;
