Идеальное интегрирующее звено.

, (2.38)

где k – коэффициент усиления, его размерность [k] = 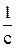(радиан в секунду),

T – постоянная времени звена, [T] = с.

Комплексный коэффициент передачи звена

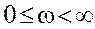, . (2.39)

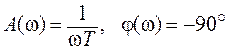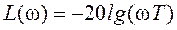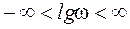, , . (2.40)

Согласно выражению (2.39) годограф комплексного коэффициента передачи инерционного звена совпадает с отрицательной частью мнимой оси. Когда частота ω = 0 его амплитуда бесконечна, с увеличением частоты она уменьшается и при 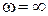годограф приходит в начало координат.

График L = L(w) логарифмической амплитудно-частотной характеристики интегрирующего звена (учитывая логарифмический масштаб по оси w) представляет собой прямую с наклоном – 20 дБ/дек во всей области частот (0£ w <¥), пересекающую ось w на частоте w = k. (Наклон -20 дБ/дек означает, что при увеличении частоты в 10 раз (на декаду) величина L(w) уменьшится на 20 дБ).

Логарифмическая фазочастотная характеристика во всей области частот равна j(w) º – 90°. На рис. 2.5 точно один под другим изображены графики ЛАХ интегрирующего звена.

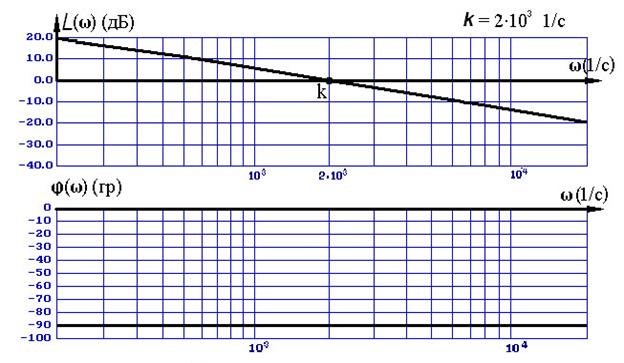
Рис. 2.5. ЛАХ идеального интегрирующего звена