Методы, основанные на использовании преобразования Лапласа
В общем случае согласно определению передаточной функции (см.(2.13)) справедливо соотношение
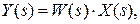
что позволяет определить формулы для вычисления изображений временных характеристик.
а)  (2.31)
(2.31)
б) 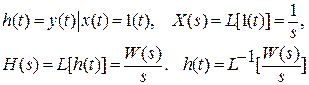 (2.32)
(2.32)
Если задана передаточная функция 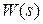 , то, используя обратное преобразование Лапласа, определяются функции
, то, используя обратное преобразование Лапласа, определяются функции 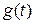 и
и 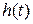 . Самым универсальным является метод, основный на применении теоремы о вычетах.
. Самым универсальным является метод, основный на применении теоремы о вычетах.
Пусть известны корни характеристического уравнения (2.15) 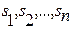 . Тогда аналогично формуле (2.16) справедливо соотношение
. Тогда аналогично формуле (2.16) справедливо соотношение
 (2.33)
(2.33)
Применяя обратное преобразование Лапласа, получим выражение, совпадающее с (2.26)
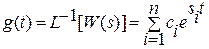 . (2.34)
. (2.34)
При разложении изображения  появляется дополнительный нулевой корень
появляется дополнительный нулевой корень 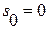 его характеристического уравнения
его характеристического уравнения 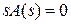 . Таким образом,
. Таким образом,
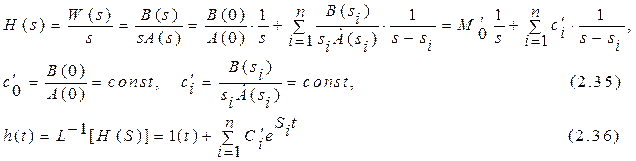
Дата добавления: 2015-07-30; просмотров: 824;
