Классический метод

Метод основан на непосредственном интегрировании дифференциальных уравнений.

Для определения импульсной переходной характеристики 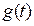интегрируют уравнение (2.11) после подстановки в него входного воздействия и его производных. Линейные системы всегда имеют нулевые начальные условия, т.е. при входное воздействие 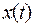отсутствует и выходная величина 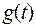и ее n-1 производных равны нулю. Дельта-функция 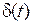на входе и ее производная приводят при 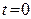к скачкообразному изменению начальных условий, а далее их действия прекращаются и правая часть уравнения (2.11) в этих условиях становится равной нулю. Поэтому рассматривают начальные условия для моментов времени 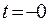, сколь угодно приближающихся к нулю слева, и 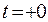– справа от нуля.

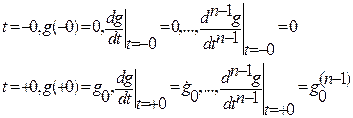(2.23,2.24)

При 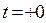не все составляющие вектора начальных условий 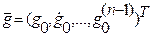должны быть равны нулю.

Величина скачка вектора 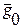зависит только от параметров системы. В первую очередь – от соотношений между величинами порядков n и m, во вторую – от коэффициентов 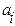и 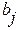уравнения (2.11). Формулы для вычисления составляющих вектора 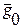можно найти в литературе (например, в )

Таким образом, импульсная переходная характеристика 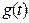определяется интегрированием линейного однородного дифференциального уравнения n-го порядка.

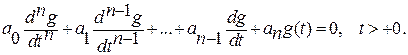(2.25)

с начальными условиями (2.24).

Общее решение уравнения (2.25) имеет вид

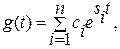(2.26)

где 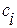- постоянные интегрирования, определяемые начальными условиями (2.24), s_i – корни характеристического уравнения системы (2.15).

Характер изменения функции 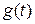зависит исключительно от характера корней s_i. Подробный анализ решения уравнения (2.25) будет проведен при изучении устойчивости САУ.

Дифференциальное уравнение для переходной характеристики 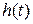получается подстановкой функции 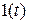и ее производных в уравнение (2.11) и интегрированием его при 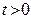. И в этом случае при 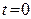происходит скачок начальных условий, т.е.

(2.27,2.28)

Формулы для вычисления 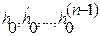можно найти в литературе, например, в .

Итак, для положительных моментов времени для переходной характеристики справедливо линейное неоднородное (с правой частью) дифференциальное уравнение n-го порядка

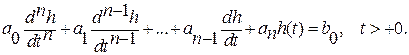(2.29)

Общее решение

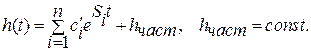(2.30)

где 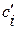– постоянные интегрирования, определяемые начальными условиями (2.27), 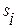– корни характеристического уравнения (2.26), 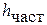– частное решение уравнения (2.28), определяемое видом его правой части.