Алгоритм минимизации при использовании D-триггера.
1. Каждому состоянию ставится в соответствие целое число Nm, равное числу переходов в состояние аm.
2. Числа Nm сортируются по убыванию.
3. Состояние с наибольшим N кодируются 00…00.
4. Следующие I состояний (I-число ЭП) кодируются 00..01, 00..10..0
5. Для кодирования оставшихся состояний используются коды, содержащие 2, затем 3 единицы и т.д., пока все состояния не будут закодированы.
В результате получаем кодирование, при котором чем больше переходов имеется в некоторое состояние am, тем меньше единиц содержится в его коде.
Большое число работ было посвящено получению такого кодирования, при котором уменьшается зависимость функции возбуждения ЭП от переменных обратной связи 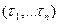 .
.
В то же время многие авторы отмечают сложность этих методов кодирования, а также трудности одновременной минимизации функции возбуждения элементов памяти и функции выходов. Поэтому на практике чаще всего используется эвристический алгоритм кодирования состояний автомата, минимизирующий суммарное число переключений элементов памяти на всех переходах автомата. При таком подходе уменьшается сложность схем, реализующих дизъюнкцию на входе ЭП, а, следовательно, минимизирующих и комбинационную схему.
Основной алгоритм:
1. Строим матрицу, состоящую из различных пар номеров таких, что в автомате S есть переход 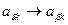

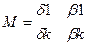
2. Переставим строки матрицы так, чтобы выполнялось условие:
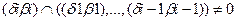 . Такую матрицу можно построить только для связного графа автомата.
. Такую матрицу можно построить только для связного графа автомата.
3. Закодируем состояние первой строки:
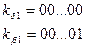
4. Вычёркиваем из матрицы М первую строку. Получим матрицу М’.
5. В начальной строке матрицы М’ один элемент уже закодирован.
6. Выберем незакодированный элемент первой строки матрицы и обозначим его 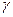 .
.
Построим матрицу М 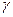 ,выбрав из М’ все строки содержащие элемент
,выбрав из М’ все строки содержащие элемент 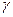 .
.
7. Пусть множество 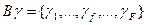 - множество всех элементов матрицы М
- множество всех элементов матрицы М 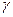 , которые уже закодированы. Они известны.
, которые уже закодированы. Они известны.
Для каждого кода k 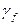 найдём
найдём 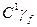 - множество кодов, соседних с кодом k
- множество кодов, соседних с кодом k 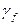 и ещё не занятых для кодирования состояний автомата. Построим множество всех возможных кодов, соседних и еще незакодированных:
и ещё не занятых для кодирования состояний автомата. Построим множество всех возможных кодов, соседних и еще незакодированных:
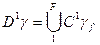
если 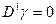 , то строим множество
, то строим множество 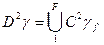 .
.
Если нет ни одного множества с незакодированными элементами, то количество ЭП выбрано неправильно.
8. Находим 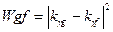 - кодовое расстояние
- кодовое расстояние
9. Находим сумму всех кодовых расстояний
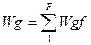
10. Выбираем код для состояния 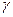 , у которого сумма кодовых расстояний Wg минимальна.
, у которого сумма кодовых расстояний Wg минимальна.
11. Из матрицы М’ вычеркиваем строки, в которых оба элемента закодированы, получаем матрицу М”. Если матрица М’ - пустая, переходим к пункту 12, иначе к пункту 5.
12. Вычисляем 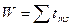 , сумму всех кодовых расстояний.
, сумму всех кодовых расстояний.
Оценкой качества кодирования рассмотренного алгоритма может служить число К
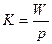 ,
,
где р - число переходов данного автомата. Чем меньше К, тем ближе полученное кодирование к соседнему.
Эксперименты показали, что К при хорошем кодировании лежит в пределах 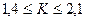 .
.
Дата добавления: 2015-07-30; просмотров: 1184;
