Метод противогоночного кодирования состояний автомата
Пусть существуют две пары двоичных кодов 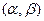 и
и 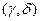 . Пары называют развязанными, если i-ый разряд кода принимает одно значение в паре
. Пары называют развязанными, если i-ый разряд кода принимает одно значение в паре 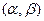 и противоположное в паре
и противоположное в паре 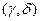 , иначе пары называются связными.
, иначе пары называются связными.
Доказана теорема, что в автомате состояние которого закодировано двоичными кодами, гонки отсутствуют, тогда и только тогда, когда для любых двух переходов 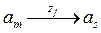 ,
, 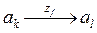 , происходящих под действием одного и того же входного сигнала, соответствующие пары кодов состояний развязаны.
, происходящих под действием одного и того же входного сигнала, соответствующие пары кодов состояний развязаны.
Алгоритм противогоночного кодирования заключается в последовательном развязывании пар переходов.
Алгоритм:
Пусть имеются состояния автомата - (am,as), (ak,al)
Значение i-го разряда в данных состояниях - 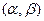 ,
, 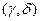 , i=1,I.
, i=1,I.
Присвоить i:=1.
1. Если при некотором i значение i-ого разряда кодов  образуют набор соответственно 0011 или 1100,то переходим к пункту 8, иначе к пункту 3.
образуют набор соответственно 0011 или 1100,то переходим к пункту 8, иначе к пункту 3.
2. Если при некотором i значение i-ого разряда  образуют один из наборов *011, 0*11, 00*1, 001*, *01*, **11, 0**1, 00**, *0*1, 0*1*, ***1, 0***, *0**, **1*, ****, то переходим к пункту 4, иначе к пункту 5.
образуют один из наборов *011, 0*11, 00*1, 001*, *01*, **11, 0**1, 00**, *0*1, 0*1*, ***1, 0***, *0**, **1*, ****, то переходим к пункту 4, иначе к пункту 5.
3. Доопределить неопределённые значения i-ого разряда до набора 0011, перейти к пункту 8.
4. Если значения i-ого разряда  образуют один из наборов *100, 1*00, 110*, …, то перейти к пункту 6. Иначе к пункту 7.
образуют один из наборов *100, 1*00, 110*, …, то перейти к пункту 6. Иначе к пункту 7.
5. Доопределить неопределённые значения i-ого разряда до набора 1100 и перейти к пункту 8.
6. Дополнить коды состояния автомата одним неопределённым разрядом и перейти к пункту 2.
8. Пары переходов (am,as), (ak,al) развязаны.
ПРИМЕР:
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | |
| Z1 | a2 | a2 | a4 | а4 | a6 | a6 | - |
| Z2 | a1 | a3 | a3 | а1 | a3 | - | - |
| Z3 | - | a5 | a7 | - | a5 | - | a7 |
 Z1: (a1,a2) (a2,a2) (a3,a4) (a4,a4) (a5,a6) (a6,a6)
Z1: (a1,a2) (a2,a2) (a3,a4) (a4,a4) (a5,a6) (a6,a6)
(а1,а2) (а2,а2) – Состязания некритические
(а1,а2) (а3,а4) – Состязания критические
Рассмотрим всевозможные пары Z1.
Вводим код длиной 1.
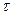 1 1
| 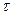 2 2
| 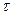 3 3
| 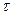 4 4
| |
| a1 | - | |||
| a2 | ||||
| a3 | ||||
| a4 | - | |||
| a5 | ||||
| a6 | - | - | ||
| a7 | - | - | - |
Сейчас все пары развязаны для z1.
Аналогично проверяем все пары Z2, Z3.
Z2=(a1,a1) (a2,a3) (a3,a3) (a4,a1) (a5,a3)
Z3=(a2,a5) (a3,a7) (a5,a5) (a7,a7)
Длина кода, полученная в результате применения алгоритма противогоночного кодирования, в большинстве случаев оказывается не минимальной, поскольку при введении нового разрядного кода могут развязаться пары переходов, которые уже были развязаны ранее. В связи с этим необходимо минимизировать длину получаемых кодов. Для этого исключается один из разрядов кодов, в результате чего некоторые пары могут оказаться связанными, поэтому применим алгоритм развязывания переходов и пробуем исключить еще один разряд и т.д. до тех пор, пока изменить длину кода возможно.
 
| 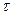 1 1
| 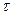 2 2
| 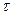 3 3
| 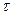 4 4
| 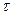 5 5
|
| a1 | - | ||||
| a2 | |||||
| a3 | - | ||||
| a4 | - | - | |||
| a5 | |||||
| a6 | - | - | |||
| a7 | - | - | - |
Дальнейшее вычёркивание приведёт к добавлению 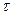 6. Получим код, в котором все пары развязаны и длина этого кода минимальна.
6. Получим код, в котором все пары развязаны и длина этого кода минимальна.
Дата добавления: 2015-07-30; просмотров: 1697;
