Свойства математического ожидания
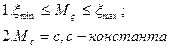
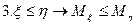
4.Константа-множитель выносится из-под знака математического ожидания.
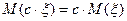
5. Математическое ожидание от алгебраической суммы любых случайных величин равно алгебраической сумме их математических ожиданий.

а) для дискретных
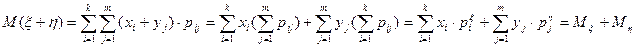
б) для непрерывных
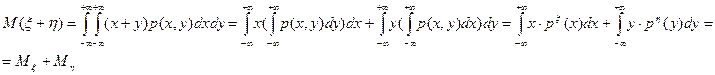 Следствие:
Следствие:
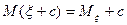
6. Если случайные величины ξ и η – независимы, то мат. ожидание от произведения случайных величин равно произведению их мат. ожиданий.
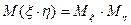
а) для дискретных

б) для непрерывных
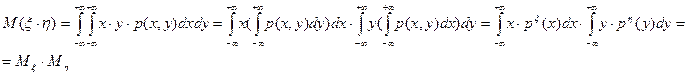
7. Неравенство Йенсена
Если функция 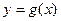 выпукла вниз, то для любой случайной величины ξ
выпукла вниз, то для любой случайной величины ξ
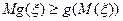
Доказательство:
Предположим, что функция g(x) дважды дифференцируема по формуле Тейлора:

Вторая производная выпуклых вниз функций всегда положительная:
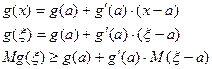
Пусть 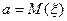
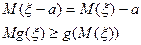
8. Неравенство Ляпунова
Для любых положительных α,β; 0<α<β
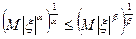
Доказательство:
 , т.к.
, т.к. 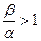 , то функция выпукла вниз, значит применимо неравенство Йенсена
, то функция выпукла вниз, значит применимо неравенство Йенсена
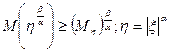
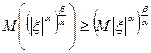
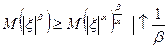
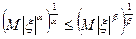
9. Неравенство Коши-Буняковского
Для любых двух случайных величин ξ и η
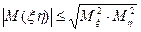
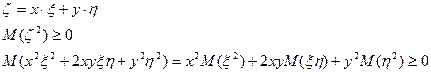
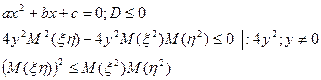
10. Неравенство Гёльдера
p>1,q>1 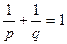
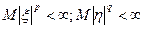 тогда
тогда 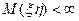

11. Неравенство Минковского
Если 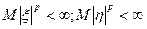 , р>1
, р>1
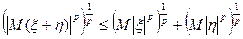
Задача: По мишени делают 3 выстрела. Результаты этих выстрелов не зависят друг от друга. Вероятность попадания при первом 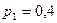 , при втором
, при втором 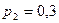 , при третьем
, при третьем 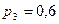 .
.
Рассматривается случайная величина, характеризующая число попаданий в мишень. Найти её мат. ожидание.
1.
| ξ | 0 | 1 | 2 | 3 |
| p | 0,168 | 0,436 | 0,324 | 0,072 |
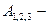 попадание при 1,2,3 выстреле соответственно.
попадание при 1,2,3 выстреле соответственно.
а) 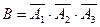
б) 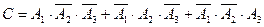
в) 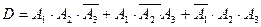
г) 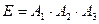
2. 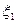 - число попаданий при первом выстреле
- число попаданий при первом выстреле
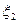 - число попаданий при втором выстреле
- число попаданий при втором выстреле
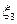 - число попаданий при третьем выстреле
- число попаданий при третьем выстреле
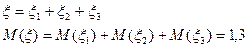
Дата добавления: 2015-07-30; просмотров: 1399;
