Промерзание грунта на допустимую глубину при использовании теплоизоляционного покрытия
Для решения данной задачи рассмотрим модель «теплоизоляционное покрытие-промерзший грунт-талый грунт», изображенную на рис. 2.3.
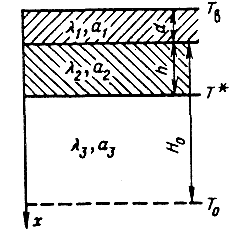
Рис.2.3. Тепловая модель «теплоизоляционное покрытие — промерзший грунт — талый грунт»
Дифференциальные уравнения теплопроводности для установившегося режима соответственно для теплоизоляционного покрытия, промороженного слоя грунта и талого будут иметь вид
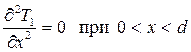 (2.61)
(2.61)
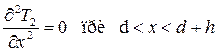 (2.62)
(2.62)
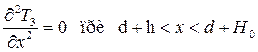 (2.63)
(2.63)
Так как рассматривается установившийся режим, то для простоты решения (не уменьшая точность) воспользуемся граничным условием первого рода
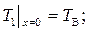 (2.64)
(2.64)
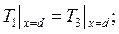 (2.65)
(2.65)
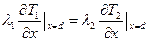 (2.66)
(2.66)
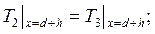 (2.67)
(2.67)
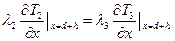 (2.68)
(2.68)
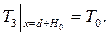 (2.69)
(2.69)
Общие решения уравнений (2.61), (2.62) и (2.63) будем искать в виде:
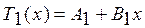 (2.70)
(2.70)
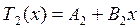 (2.71)
(2.71)
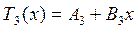 (2.72)
(2.72)
Подставляя общие решения (2.70)-(2.72) в начальное и граничные условия (2.64)-(2.69), получим систему уравнений для определения постоянных коэффициентов A1 , А2, A3, В1, В2 и В3.
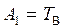 (2.73)
(2.73)
 (2.74)
(2.74)
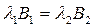 (2.75)
(2.75)
 (2.76)
(2.76)
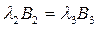 (2.77)
(2.77)
 (2.78)
(2.78)
Выражение (2.78) можно представить в виде:
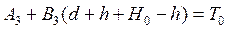
или
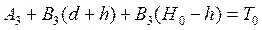
откуда с учетом (2.76) имеем
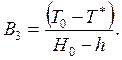 (2.79)
(2.79)
Из (2.77) с учетом (2.79) получим
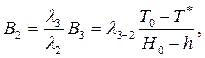 (2.80)
(2.80)
где
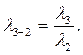
Из (2.75) с учетом (2.80) получим
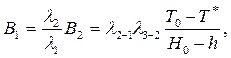 (2.81)
(2.81)
Из (2.74) с учетом (2.73), (2.80) и (2.81) получим
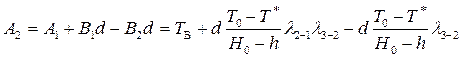 (2.82)
(2.82)
Из (2.78) с учетом (2.79) получим
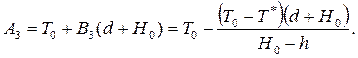 (2.83)
(2.83)
Произведем сшивание решений (2.71) в (2.72) на границе (d + h)
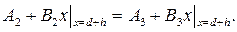
или
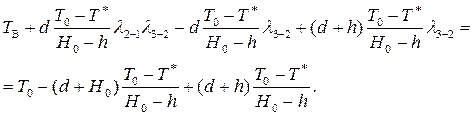
откуда после преобразований получим
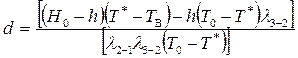 (2.84)
(2.84)
Вводя обозначения
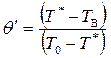 и
и 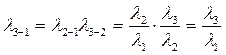
из (2.84) получим
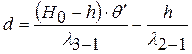 (2.85)
(2.85)
Условие предотвращения промерзания грунта на глубину более чем h согласно будет иметь вид:
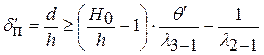 (2.85)
(2.85)
или
 (2.86)
(2.86)
Выражение (2.86) получено без учета фазового перехода «вода-лед» в промерзшем слое породы и поэтому весьма грубо позволяет оценить необходимую толщину теплоизоляционного покрытия. Это выражение дает завышенное значение для d, так как в общем решении уравнения (2.71) не учтена теплота замерзания поровой воды в породе при ее промерзании на глубину h.
Точное значение величины d можно получить, если левые части выражений (2.85) и (2.86) умножим на некоторый поправочный коэффициент Кф, численное значение которого меньше единицы. Коэффициент Кф характеризует, во сколько раз количество тепла Qох, затраченное на охлаждение промерзшего слоя породы от температуры Т* при х = d + h до некоторой отрицательной температуры Т│x=d при х = d, меньше, чем количество тепла Qф, затраченное на фазовый переход «вода-лед» в слое связной породы толщиной h.
Величины Qох и Qф для 1 м поверхности уступов карьеров соответственно будут
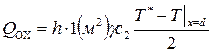 (2.87)
(2.87)
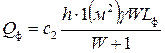 (2.88)
(2.88)
где γ — плотность связной породы, кг/м3;
c2 — удельная теплоемкость мерзлой связной породы, Дж/(кг∙К);
W — влажность связной породы в долях единицы;
Lф— удельная теплота плавления льда; Lф = 3,32·105 Дж/кг.
Значение Т│x=d можно получить, подставив в выражение (2.71) величины А2 и В2. С учетом (2.87) и (2.88) величина Кф будет
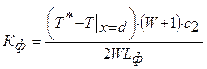 (2.89)
(2.89)
Необходимая толщина теплоизоляционного покрытия d', обеспечивающая предотвращение промерзания грунта влажностью W не более, чем на глубину h, согласно (2.86) и (2.88) будет
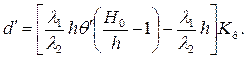 (2.90)
(2.90)
ТЕМА №3. НАМОРАЖИВАНИЕ ПОРОД ПРИ СТРОИТЕЛЬСТВЕ ПОДЗЕМНЫХ СООРУЖЕНИЙ И ШАХТ
Дата добавления: 2015-07-30; просмотров: 724;
