Полное предотвращение промерзания грунта при использовании теплоизоляционных покрытий
Рассмотрим случай, когда теплоизоляционное покрытие обеспечивает полное предотвращение промерзания грунта.
Для определения толщины теплоизоляционного покрытия (d) и его свойств, необходимых для полного предотвращения промерзания грунта, рассмотрим модель, изображенную на рис. 2.2.
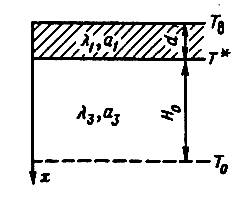
Рис. 2.2. Тепловая модель «промерзший грунт — талый фунт»
Дифференциальные уравнения теплопроводности при установившемся режиме для теплоизоляционного покрытия и непромерзшего грунта соответственно имеют вид
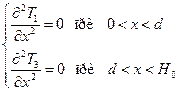 (2.41)
(2.41)
Граничные условия задачи запишем в виде
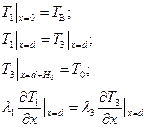 (2.42)
(2.42)
Общие решения дифференциальных уравнений (2.41) будем искать в виде:
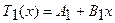 (2.43)
(2.43)
 (2.44)
(2.44)
Подставляя решения (2.43) и (2.44) в граничные условия (2.42), получим систему уравнений для определения постоянных коэффициентов А1, A2, В1 и В3.
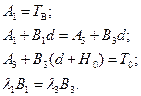 (2.45)
(2.45)
Из решения системы (2.45) получим
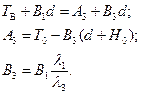
откуда
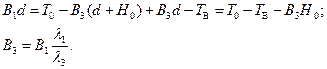 (2.46)
(2.46)
Решая совместно систему (2.46), получим
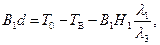
откуда
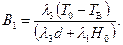 (2.47)
(2.47)
Подставляя значения A1 и В1 из (2.45) и (2.47) в (2.43) получим уравнение для оценки поля температур в теплоизоляционном покрытии
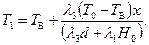 (2.48)
(2.48)
Если толщина и свойства теплоизоляционного покрытия обеспечивают полное предотвращение промерзания грунта, то согласно (2.48) при х = d получим

откуда условие полного предотвращения промерзания грунта примет вид:
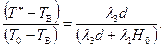 (2.49)
(2.49)
Обозначив
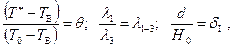
из (2.49) получим условие полного предотвращения промерзания грунта в безразмерном виде:
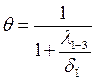 или
или 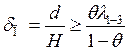 (2.50)
(2.50)
Условие (2.50) справедливо для случая, когда теплоизоляционное покрытие не водонасыщено.
Условие (2.50) получено для случая, когда на поверхности грунта теплообмен задан граничными условиями первого рода. Если на поверхности грунта заданы граничные условия третьего рода, система граничных условий задачи о полном предотвращении промерзания грунта будет иметь вид:
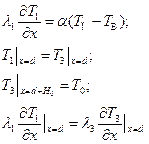 (2.51)
(2.51)
где α — коэффициент теплоотдачи, Вт/(м2·К);
Тп — температура поверхности теплоизоляционного покрытия, К.
Решение дифференциальных уравнений (2.41) приграничных условиях (2.51) аналогично предыдущей задаче будем искать в виде (2.43) и (2.44)
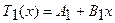 ,
,
 .
.
Подставив решения (2.43) и (2.44) в граничные условия (2.51), получим систему уравнений для определения постоянных коэффициентов А1, A2, В1 и В3.
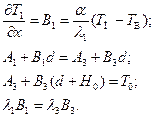
откуда
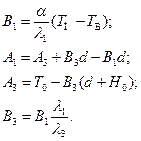 (2.52)
(2.52)
Решая систему (2.52) относительно А1 , получим
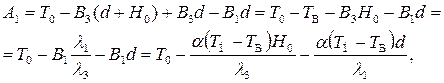
или, обозначив относительные коэффициенты теплоотдачи 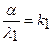 и
и 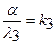 , получим
, получим
 (2.53)
(2.53)
Подставляя значения В1 из (2.52) и А1 из (2.53) в общее решение
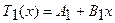 ,
,
 ,
,
получим уравнение для оценки поля температур в теплоизоляционном покрытии при граничных условиях третьего рода
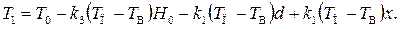 (2.54)
(2.54)
При х = d из (2.54) получим
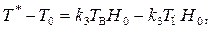 (2.55)
(2.55)
откуда
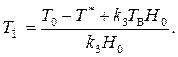 (2.56)
(2.56)
При х = 0 общее решение (2.43) примет вид:
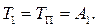 (2.57)
(2.57)
Согласно (2.53) и (2.57) имеем
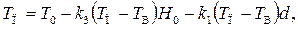
откуда
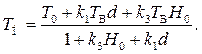 (2.58)
(2.58)
Приравнивая правые части выражений (2.56) и (2.58), получим

или, поделив почленно на Н0, будем иметь условие полного предотвращения промерзания грунта при граничных условиях третьего рода
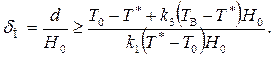 (2.59)
(2.59)
Обозначив 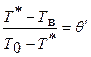 , получим из (2.59) условие полного предотвращения промерзания грунта в безразмерном виде
, получим из (2.59) условие полного предотвращения промерзания грунта в безразмерном виде
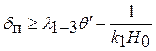 (2.60)
(2.60)
где
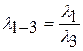 .
.
Дата добавления: 2015-07-30; просмотров: 636;
