Тепловой расчет формирования одиночного ледопородного цилиндра
При замораживании вокруг каждой замораживающей колонки формируется температурное поле, изотермы которого представляют собой в плане концентрические окружности. Температура породы непосредственно у замораживающей колонки будет на 3-5 К выше температуры хладоносителя. В радиальном направлении от центра каждой замораживающей скважины темпратура грунта повышается. На внешней поверхности каждого ледопородного цилиндра температура равна температуре фазового перехода, а далее повышается вплоть до естественной температуры массива. С течением времени замораживания радиус каждого ледопородного ограждения увеличивается, но не беспредельно. При некотором критическом радиусе количество холода, поступающего в массив, окружающий ледопородный цилиндр, будет скомпенсировано теплом геотермического теплового потока, направленного к замораживающей скважине. Из этого следует, что для образования ледопородных ограждений расстояние между смежными замораживающими скважинами должно быть значительно меньше удвоенного критического радиуса ледопородного ограждения. Только при этом условии возможно смыкание отдельных ледопородных цилиндров и образование единого ледопородного ограждения.
Породы в объеме ледопородного цилиндра или ледопородного ограждения являются мерзлыми, далее в радиальном направлении следует зона охлажденных пород и затем зона пород с нормальной для данного района температурой.
Как и ранее, условимся обозначить индексом 2 параметры, относящиеся к мерзлым породам, а индексом 3 — к талым породам. Температуру фазового перехода обозначим через Т*, начальную естественную температуру массива — через Т0, а температуру рассола в замораживающей колонке — через Тр.
В процессе формирования одиночного ледопородного цилиндра холод, поступающий от замораживающей колонки, расходуется на охлаждение массива в объеме замерзшей породы от температуры Т0 до температуры Т* и далее до температуры Тр; на теплоту фазового перехода; на понижение температуры массива в зоне охлажденных пород от температуры Т0 до температуры Т*.
Для оценки времени формирования одиночного ледопородного цилиндра предположим, что замораживающая скважина является обособленной, вода в породе не фильтрует и теплопоток, обусловленный геотермическим градиентом, отсутствует.
В математической постановке задача может быть сформулирована следующим образом: в бесконечном пространстве с температурой Т0 и свойствами талого грунта имеется цилиндрическая полость, равная радиусу замораживающей колонки rк; в момент времени τ= 0 на поверхности полости устанавливается температура, равная температуре Тр; в результате охлаждения массива вокруг цилиндрической полости образуется ледопородный цилиндр переменного радиуса rц = f (τ); подвижная граница ледопородного цилиндра имеет температуру фазового перехода Т* ; на этой границе выделяется теплота фазового перехода Lф, Дж/кг.
При формировании одиночного ледопородного цилиндра имеет место теплоперенос, обусловленный движением тепла к замораживающей колонке в радиальном направлении. Одновременно за счет термодиффузии имеет место массоперенос влаги в том же направлении от мест с более высокой температурой в места более холодные.
Процесс тепло- и массопереноса вокруг замораживающей колонки описывается системой дифференциальных уравнений:
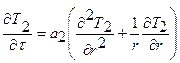 при rк <r<rц (3.1)
при rк <r<rц (3.1)
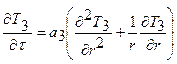 при rц <r<∞ (3.2)
при rц <r<∞ (3.2)
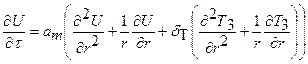 при rц <r<∞ (3.3)
при rц <r<∞ (3.3)
Для определения вокруг замораживающей колонки поля температур и поля влагосодержания необходимо решить дифференциальные уравнения (3.1)-(3.3) при следующих начальных и граничных условиях:
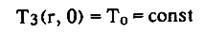 (3.4)
(3.4)
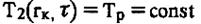 (3.5)
(3.5)
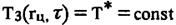 (3.6)
(3.6)
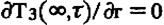 (3.7)
(3.7)
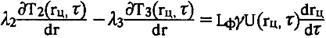 (3.8)
(3.8)
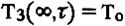 (3.9)
(3.9)
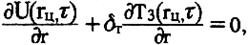 (3.10)
(3.10)
где а — коэффициент температуропроводности породы, м/с; аm — коэффициент абсолютной термодиффузии влаги, м /с; λ — коэффициент теплопроводности породы, Дж/(м∙с∙К); δT— относительный коэффициент термодиффузии влаги, 1/К; U — влагосодержание породы, кг/кг; γ — плотность породы, кг/ м.
Решения дифференциальных уравнение (3.1)-(3.3) при краевых условиях (3.4)-(3.10) имеют вид:
• для оценки температурного поля в мерзлой зоне
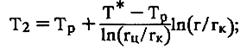 (3.11)
(3.11)
• для оценки температурного поля в талой зоне
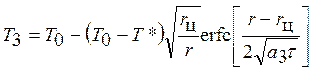 (3.12)
(3.12)
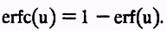
• для оценки поля влагосодержания в талой зоне

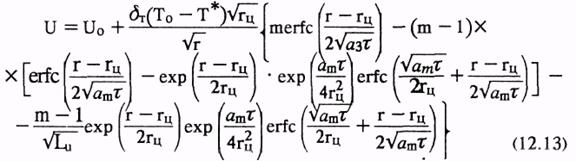
• для оценки влагосодержания на границе фазового перехода при r = rц
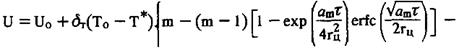
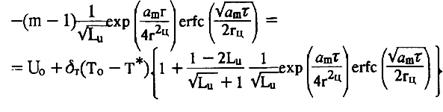 (3.14)
(3.14)
где U0 — начальное влагосодержание породы, кг/кг; m = 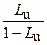 ; Lu — критерий Лыкова,
; Lu — критерий Лыкова, 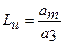 .
.
Фронт продвижения границы фазового перехода гц определяют численным методом из уравнения
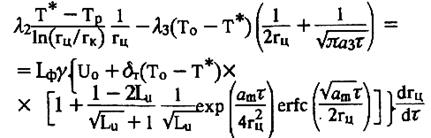 (3.15)
(3.15)
Для определения характера распределения температурного поля в мерзлой и талой зонах и поля влагосодержания необходимо из уравнения (3.15) определить значение rц при заданном τ, а затем по формулам (3.11)-(3.14) определить искомые величины. Чтобы определить время образования одиночного ледопородного цилиндра радиусом rц необходимо в уравнении (3.15) вместо rц подставить его численное значение.
Дата добавления: 2015-07-30; просмотров: 799;
