Это уравнение Нернста – Эйнштейна связывает коэффициент диффузии иона с его электрической подвижностью.
18.3. Диффузионный потенциал.
Пусть электролит 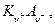 который полностью диссоциирует на ионы KZ+ и AZ- ,диффундирует из области с концентрацией C1 в область с концентрацией C2 ( C1 >C2 ). Если D+ = D-, то процесс не отличается от обычной диффузии незаряженных частиц, но если D+ ≠ D-, то возникают специфические явления.Дело в том. что более подвижный ион обгоняет менее подвижный до тех пор, пока образовавшееся электрическое поле не уравняет их скорости (
который полностью диссоциирует на ионы KZ+ и AZ- ,диффундирует из области с концентрацией C1 в область с концентрацией C2 ( C1 >C2 ). Если D+ = D-, то процесс не отличается от обычной диффузии незаряженных частиц, но если D+ ≠ D-, то возникают специфические явления.Дело в том. что более подвижный ион обгоняет менее подвижный до тех пор, пока образовавшееся электрическое поле не уравняет их скорости ( 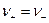 ) и уже в этом случае можно говорить об общем потоке электролита, однако это не обычный поток диффузии, поскольку между двумя областями раствора с концентрациями С1 и С2 устанавливается стационарная разность потенциалов
) и уже в этом случае можно говорить об общем потоке электролита, однако это не обычный поток диффузии, поскольку между двумя областями раствора с концентрациями С1 и С2 устанавливается стационарная разность потенциалов
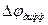 - диффузионный потенциал.
- диффузионный потенциал.
Если уравнение Нернста – Эйнштейна справедливо при конечных концентрациях ионов KZ+ и AZ- , то для потоков катионов и анионов
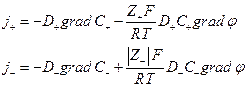
Скорость перемещения иона 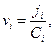 но в стационарных условиях
но в стационарных условиях
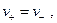 т.е.
т.е. 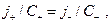 т.е.
т.е.
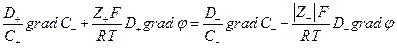
Так как 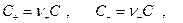 то
то
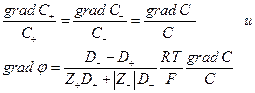
Интегрирование в пределах от С1 до С2 дает
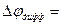
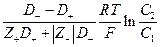
18.4. Удельная и эквивалентная электропроводности в растворах электролитов.
Электропроводность раствора электролита обеспечивается за счет потоков миграции ионов, присутствующих в растворе, но эксперимент необходимо проводить так, чтобы не возникал градиент химического потенциала, что достигается использованием переменного тока. Как и для обычных проводников, сопротивление растворов рассчитывается по формуле
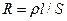
где ρ – удельное сопротивление, l - расстояние между электродами, S – площадь электродов. Величина  1/ρ = χ называется удельной электропроводностью, ее размерность Ом-1·м-1 (Ом-1·см-1) или Сн/м (Сн/см), где
1/ρ = χ называется удельной электропроводностью, ее размерность Ом-1·м-1 (Ом-1·см-1) или Сн/м (Сн/см), где
Сн – симекс. Удельная электропроводность характеризует электропроводность объема раствора, заключенного между двумя параллельными электродами, имеющими площадь 1 м2 (или 1 см2) и расположенными на расстоянии 1 м
(или 1 см) друг от друга. При С → 0 величина χ стремится к удельной электропроводности чистой воды (примерно 10-5 Сн/м). С ростом концентрации электролита χ сначала возрастает в связи с увеличением числа ионов в растворе, однако с ростом концентрации начинает проявляться ион-ионное взаимодействие, приводящее к замедлению движения ионов, а также к их ассоциации. Поэтому почти всегда зависимость удельной электропроводности от концентрации электролита проходит через максимум.
Чтобы выделить эффект ион – ионного взаимодействия удельную электропроводность χ делят на Z+ν+C, где С – число молей в единице объема
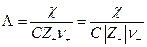
Величина Λ называется эквивалентной электропроводностью: она представляет собой электропроводность объема электролита, содержащего 1 г-экв растворенного вещества и находящегося между двумя параллельными электродами, расположенными на расстоянии 1 м (1 см) друг от друга. Чем меньше концентрация раствора, тем больший его объем приходится на 1 г-экв и, следовательно, тем большая площадь электродов покрыта раствором. Таким образом, уменьшение числа носителей тока в единице объема раствора с его разведением компенсируется увеличением поперечного сечения. Если бы потоки миграции не зависели бы от ион-ионного взаимодействия, то Λ оставалась бы постоянной при всех концентрациях. В реальных системах эквивалентная электропроводность зависит от концентрации, а при С →0 величина Λ стремится к своему предельному значению Λ0, отвечающему отсутствию ион-ионного взаимодействия. В растворах слабых электролитов, где ион-ионное взаимодействие приводит к образованию нейтральных молекул уже при очень низких концентрациях ионов, выход Λ на предельное значение экспериментально наблюдать не удается.
Пример. Электропроводности pаствора КСl при 25 0С.
| С, моль/л | моль/м3 | χ, См/м | Λ, См·м2/моль |
| 103 | 11,19 | 0,01119 | |
| 0,1 | 102 | 1,289 | 0,01289 |
| 0,01 | 0,1413 | 0,01413 | |
| 0,001 | 0,01469 | 0,01469 | |
| 0,0001 | 10-1 | 0,001489 | 0,01489 |
В растворе электролита ток переносится катионами и анионами, поэтому при
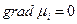 для плотности тока можно записать
для плотности тока можно записать
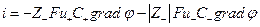
Для слабого электролита со степенью диссоциации α по условию электронейтральности раствора имеем
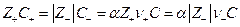 и
и
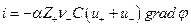
С другой стороны, по закону Ома
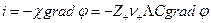
Следовательно,
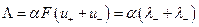
где величины 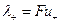 и
и 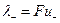 называются ионными электропроводностями (или подвижностями ) ионов. В растворах сильных электролитов α =1 и
называются ионными электропроводностями (или подвижностями ) ионов. В растворах сильных электролитов α =1 и
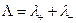
а при бесконечном разведении, когда α→1
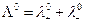
где 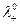 и
и 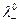 предельные электропроводности (или подвижности) ионов.
предельные электропроводности (или подвижности) ионов.
Последние три уравнения представляют собой закон Кольрауша, сущность которого состоит в том, что в растворе электролита катионы и анионы переносят электрический ток независимо друг от друга.
В теории Аррениуса предполагалось (гл.12), что подвижность ионов не зависит от концентрации, при этом допущении
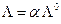
однако это справедливо только для разбавленных растворов слабых электролитов. Для последних с учетом закона разведения Оствальда (см. гл.12) можно показать, что 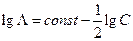
но для разбавленных растворов сильных электролитов Кольраушем было получено эмпирическое соотношение
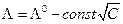
которое находится в противоречии с теорией Аррениуса.
18.5. Числа переноса ионов.
Согласно закону Кольрауша эквивалентная электропроводность определяется суммой электропроводностей катиона и аниона, следовательно для нахождения подвижности отдельного иона необходимо дополнительно определить долю тока, переносимую ионами данного вида. Эта доля и называется числом переноса ионов. Для бинарного электролита число переноса
катиона:
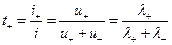
аниона:
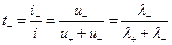
В таком растворе, очевидно, 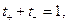 а при подстановке величин
а при подстановке величин
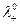 и
и 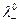 получаем предельные числа переноса
получаем предельные числа переноса 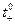 и
и 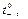 которые определяют долю тока, переносимую катионами и анионами при отсутствии ион-ионного взаимодействия и, вообще говоря,
которые определяют долю тока, переносимую катионами и анионами при отсутствии ион-ионного взаимодействия и, вообще говоря, 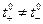 .
.
Существуют следующие экспериментальные методы определения чисел переноса.
1. Метод Гитторфа, основанный на определении концентрации электролита у катода и у анода после пропускания через раствор определенного количества электричества.
2. Метод движущейся границы, основанный на смещении границы раздела двух растворов, имеющих общий ион, после пропускания через систему определенного количества электричества.
3. Измерение диффузионного потенциала (см. следующую главу) поскольку 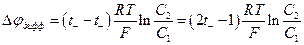
Из эксперимента следует, что числа переноса зависят от концентрации электролита, а экстраполяция на нулевую концентрацию дает предельные числа переноса 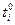 . Эти величины для водных растворов хлоридов металлов следующие (25 0С)
. Эти величины для водных растворов хлоридов металлов следующие (25 0С)
| Электролит | LiCl | NaCl | KCl | RbCl | CsCl |
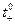
| 0,336 | 0,396 | 0,490 | 0,505 | 0,503 |
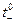
| 0,664 | 0,604 | 0,510 | 0,495 | 0,497 |
Если электролит полностью диссоциирован, то наблюдаются следующие закономерности зависимости ti от концентрации. Если 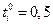 , то при увеличении концентрации ti практически не изменяется. Если
, то при увеличении концентрации ti практически не изменяется. Если 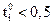 , то с ростом концентрации число переноса уменьшается, а если
, то с ростом концентрации число переноса уменьшается, а если 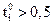 число переноса увеличивается. Повышение же температуры мало влияет на число переноса:
число переноса увеличивается. Повышение же температуры мало влияет на число переноса:
| Электролит | 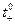 при температуре ( 0С) при температуре ( 0С)
| |||
| LiCl | 0,321 | 0,336 | 0,347 | 0,352 |
| NaCl | 0,393 | 0,396 | 0,404 | 0,406 |
| KCl | 0,498 | 0,490 | 0,487 | 0,479 |
18.6. Предельная электропроводность ионов.
Предельная эквивалентная электропроводность раствора электролита и предельные числа переноса позволяют определить предельные электропроводности отдельных ионов :
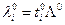
Пример. Предельные электропроводности ионов в воде при различных температурах.
| Ион | 
| |||||
| 0 0 | 18 0 | 25 0 | 45 0 | 100 0 | ||
| Li+ | 19,4 | 32,8 | 38,7 | 58,0 | ||
| Na+ | 26,5 | 42,8 | 50,1 | 73,7 | ||
| K+ | 40,7 | 63,9 | 73,5 | 103,5 | ||
| Rb+ | 43,9 | 66,5 | 77,8 | 108,6 | - | |
| Cs+ | 44,0 | 67,0 | 77,3 | 107,5 | - | |
| H+(H3O+) | 349,8 | 441,4 | ||||
| F- | - | 47,4 | 55,4 | - | - | |
| Cl- | 41,0 | 66,0 | 76,4 | 108,9 | ||
| Br- | 42,6 | 68,0 | 78,1 | 110,7 | - | |
| I- | 41,4 | 66,5 | 76,8 | 108,6 | - | |
| CH3COO- | 20,1 | 35,0 | 40,9 | - | - | |
| OH- | 198,3 | - | ||||
В поведении ионов при бесконечном разведении имеются две закономерности : 1) увеличение подвижности при повышении температуры; 2) наличие максимума на зависимости 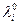 от кристаллографического радиуса иона. Для качественного объяснения можно провести аналогию между миграцией иона под действием электрического поля и движением макроскопического шарика в вязкой жидкости. Согласно закону Стокса скорость движения v твердого шарика в вязкой жидкости под действием силы Ф выражается уравнением :
от кристаллографического радиуса иона. Для качественного объяснения можно провести аналогию между миграцией иона под действием электрического поля и движением макроскопического шарика в вязкой жидкости. Согласно закону Стокса скорость движения v твердого шарика в вязкой жидкости под действием силы Ф выражается уравнением :
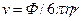
где η – вязкость жидкости, r – радиус шарика. Сила, действующая на заряд
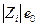 (е0 – заряд электрона) в поле Х равна
(е0 – заряд электрона) в поле Х равна 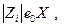 а средняя скорость движения иона в бесконечно разбавленном растворе
а средняя скорость движения иона в бесконечно разбавленном растворе 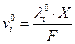 . Отсюда с использованием уравнения Стокса получаем:
. Отсюда с использованием уравнения Стокса получаем:
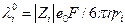
Ионы в растворе окружены гидратной оболочкой, которая движется вместе с ионом. Поскольку ион небольшого кристаллографического радиуса (Li+) гидратирован в большей степени, чем, например, Na+ или К+ , то различие в радиусах гидратированных ионов сравнительно невелико. Можно, рассчитав ri по последней формуле, вычислить объем гидратированного иона, затем за вычетом кристаллографического объема иона, определить объем гидратной оболочки VS
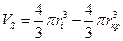
Так как объем молекулы воды составляет величину около 30 Ǻ3, то не составляет труда вычислить среднее число молекул воды 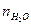 в гидратной оболочке :
в гидратной оболочке :
| Ион | Na+ | Li+ | Be2+ | Mg2+ | Ca2+ | Sr2+ | Ba2+ | Zn2+ | La3+ |
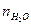
| 13-14 | 9-10 | 13-14 |
Увеличение электропроводности с ростом температуры с уменьшением вязкости среды и правило Вальдена Писаржевского 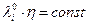 должно быть справедливо, если в данном интервале температур ri = const .
должно быть справедливо, если в данном интервале температур ri = const .
Пример. Ацетат – ион в воде
| t, 0C | ||||||||

| 0,366 | 0,368 | 0,366 | 0,368 | 0,369 | 0,368 | 0,369 | 0,369 |
Для других растворителей правило Вальдена также справедливо.
С помощью уравнения Нернста-Эйнштейна можно увязать коэфициент диффузии иона при С→ 0 с предельной электропроводностью иона :
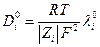
а также получить уравнение Стокса-Эйнштейна :
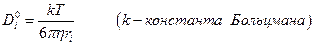
Ионы водорода и гидроксила обладают более высокой подвижностью, чем другие ионы, очевидно, что механизм миграции здесь другой.
Заметим, во-первых, протон локализуется на молекуле воды, образуя ион гидроксония Н3О+, во-вторых, ион гидроксония окружен гидратной оболочкой из 3-4 молекул воды, образуя комплекс Н9О4+. Мало вероятно, что такой комплекс будет более подвижен, чем гидратированный ион Na+. Поэтому предлагается эстафетный или гротгусовский механизм перемещения протона : перескок протона от Н3О+ к ориентированной соответствующим образом молекуле воды

Аномально высокая подвижность ионов гидроксила также объясняется перескоком протона:
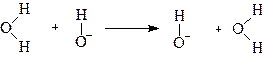
Так как протон в молекуле воды связан более прочно, чем в ионе гидроксония, то подвижность ионов гидроксила оказывается ниже, чем подвижность иона водорода.
18.7. Ионная атмосфера и зависимость электропроводности от концентрации.
Дебай и Гюккель объяснили закон Кольрауша 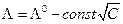 наличием ионной атмосферы (см. гл.12), плотность которой увеличивается с повышением концентрации электролита. В неравновесных условиях существование ионной атмосферы обусловливает два эффекта, тормозящих движение центрального иона, которые называются электрофоретическим или релаксационным эффектами.
наличием ионной атмосферы (см. гл.12), плотность которой увеличивается с повышением концентрации электролита. В неравновесных условиях существование ионной атмосферы обусловливает два эффекта, тормозящих движение центрального иона, которые называются электрофоретическим или релаксационным эффектами.
Электрофоретический эффект связан с тем, что ион под действием внешнего элетрического поля перемещается не в неподвижной среде, а в потоке движущихся навстречу ему противоионов, составляющих ионную атмосферу. Следовательно, из предельной подвижности иона следует вычесть подвижность ионной атмосферы, которую можно рассчитать, подставив радиус ионной атмосферы (гл. 12) в уравнение  , полученное нами в предыдущем параграфе.
, полученное нами в предыдущем параграфе.
Релаксационный эффект обусловлен конечным временем разрушения ионной атмосферы. В результате этого центр заряда ионной атмосферы в неравновесных условиях оказывается смещенным на некоторое расстояние позади от движущегося центрального иона. Таким образом возникает некоторая тормозящая электростатическая сила.
Онзагер показал теоретически, что для электролита типа 1 – 1 зависимость электропроводности от концентрации можно представить выражением
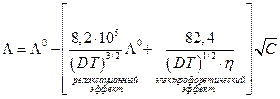
Оценка показывает , что электрофоретический эффект дает примерно 2/3 общего понижения электропроводности из-за ион-ионного взаимодействия, а на долю релаксационного эффекта приходится около 1/3 от 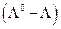 .
.
Теория Дебая –Гюккеля-Онзагера позволяет интерпретировать ряд экспериментальных фактов. В 1927 году Вин обнаружил, что при напряженностях поля порядка 200000 – 400000 В/см после резкого возрастания электропроводность выходит на свое предельное значение Λ0, что находится в противоречии с законом Ома. Но согласно теории Дебая –Гюккеля-Онзагера в этих условиях скорость движения иона становится настолько большой, что ионная атмосфера не успевает образовываться и ее тормозящее действие исчезает. Теоретическая оценка величины напряженности поля дает значение, соответствующее экспериментально наблюдаемому.
В 1928 г. Дебай и Фалькенхаген показали, что при достаточно высокой частоте переменного тока вззаимное смещение иона и ионной атмосферы настолько мало, что ионная атмосфера практически симметрична и эффект релаксации должен исчезнуть. Действительно для солей типа 1 – 1 при С = 0,001 эффект Дебая – Фалькенхагена проявляется при частоте 109 Гц. Более того, увеличение электропроводности в эффекте Дебая – Фалькенхагена составляет примерно 1/3 от увеличения Λ в эффекте Вина, как это и следует из теоретической оценки.
II. Глава 19. Равновесные электрохимические системы
19.1. Электрохимический потенциал.
Если в системе присутствуют помимо незаряженных и заряженные частицы, ее энергию Гиббса необходимо представить в виде (см. гл. 5)
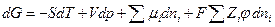
где φ –электрический потенциал в той части системы, где находятся частицы сорта i , Zi – зарядовое число частицы сорта i с учетом знака (для незаряженных Zi = 0). Тогда аналогично химическому потенциалу определим электрохимический потенциал  частицы i как
частицы i как
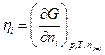
Следовательно
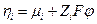
Принадлежность электрохимического потенциала к данной фазе будем обозначать надстрочным индексом (если α – некоторая фаза, то 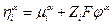 ). Если в электрохимической системе протекает некоторая химическая реакция с участием заряженных частиц, то
). Если в электрохимической системе протекает некоторая химическая реакция с участием заряженных частиц, то
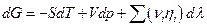
где λ –химическая переменная, и условием электрохимического равновесия будет
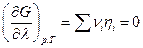
Легко показать также, что вещество будет переходить из той части системы, где его электрохимический потенциал больше, в ту часть, где его электрохимический потенциал меньше, а отсутствие переноса заряженных частиц возможно только при равенстве электрохимического потенциала в разных частях системы для данной частицы (см. также гл. 18).
В принципе электрохимические системы можно разделить на два класса : в одних энергия Гиббса химической реакции (или разность химических потенциалов) преобразуется в электрическую энергию – это т.н. химические источники тока, в других наоборот подводимая извне электрическая энергия позволяет осуществить некую химическую реакцию (или создать разность химических потенциалов) –это происходит в т.н. электролизерах.
В обоих типах электрохимических устройств катодом является тот электрод, в направлении которого движутся катионы, анодом – тот, к которому движутся анионы.
Рассмотрим два простейших примера установления электрохимического равновесия.
1. Граница двух различных металлов. В этом случае происходит выравнивание электрохимических потенциалов электронов металлов М1 и М2
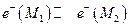
а при установлении равновесия
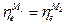
или 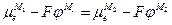
отсюда 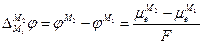
Так как химические потенциалы электрона в различных металлах неодинаковы (за химический потенциал электрона в металле обычно принимают уровень Ферми), то возникает контактная разность потенциалов Δφ
2. Граница металла М с раствором, содержащим ионы этого металла 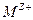 , в этом случае происходит установление равновесия:
, в этом случае происходит установление равновесия:
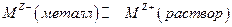
следовательно
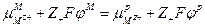
или 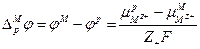
поскольку 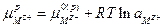 , а
, а 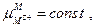 то
то
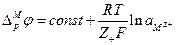
Если вместо активности иона металла в растворе использовать его концентрацию, то уравнение такого вида впервые было получено Нернстом. Однако разность потенциалов между электродом и раствором нельзя измерить, так как электрический контакт с раствором не может быть установлен в отсутствие другого электрода и, следовательно, другого электродного потенциала.
Вообще говоря, электрод представляет собой систему из двух находящихся в контакте проводников – электронного (проводник I рода) и электролита (проводник II рода).
19.2. Равновесие в электрохимической цепи. Термодинамика электрохимической цепи.
Электрохимической цепью называется система, состоящая из двух или нескольких электродов. Правильно разомкнутой электрохимической цепью называется цепь, начинающаяся и заканчивающаяся одинаковыми металлами. Электрохимическая цепь будет равновесной, если электрохимическое равновесие осуществлено на каждой фазовой границе. При этом условии электродвижущая сила Е (напряжение между металлами на концах ее ) складывается из суммы скачков потенциала на фазовых границах.
Рассмотрим электрохимическую цепь
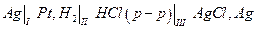
где вертикальные черточки указывают границы фаз, на которых возникает скачок электрического потенциала. Разность потенциалов на концах этой цепи Е складывается из трех скачков потенциала на границах I, II и III :
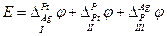
I. Устанавливается равновесие
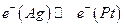
Следовательно
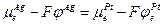 и
и
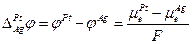
II. Устанавливается равновесие
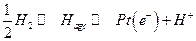
Следовательно :
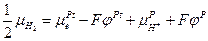
и 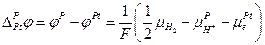
III. Устанавливается равновесие :
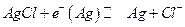
Следовательно :
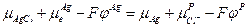
и 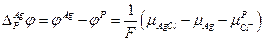
В итоге :
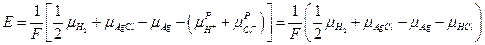
Поскольку изменение энергии Гиббса для химической реакции
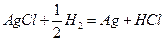 равно
равно
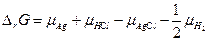 , то
, то
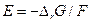
Вообще говоря, если в обратимой (равновесной) элекрохимической цепи протекает токообразующая реакция 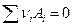 , то
, то
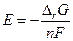
где « п » число молей электронов, прошедших в внешней цепи, когда для химической реакции 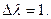 Но цепь является равновесной, если электрохимическое равновесие имеется в наличии на всех фазовых границах, если же нет, то
Но цепь является равновесной, если электрохимическое равновесие имеется в наличии на всех фазовых границах, если же нет, то 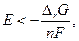 но в этом случае Е – не электродвижущая сила.
но в этом случае Е – не электродвижущая сила.
Если участники токообразующей реакции находятся в стандартных состояниях, то
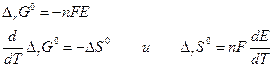
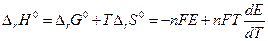
Максимальный коэффициент полезного действия равновесной электрохимической цепи можно определить как :
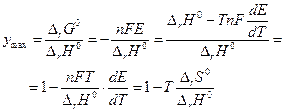
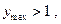 если
если 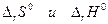 имеют разные знаки. Это значит, что электрическая работа производится не только за счет теплового эффекта химической реакции, но и за счет поглощения тепла из окружающей среды.
имеют разные знаки. Это значит, что электрическая работа производится не только за счет теплового эффекта химической реакции, но и за счет поглощения тепла из окружающей среды.
Пример.
| Электро-химическая. цепь | t, 0С | Е, В | 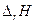 ,
ккал ,
ккал
| 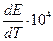 В/К
В/К
| 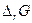 ,
ккал ,
ккал
|
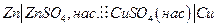
| 1,0934 | -55,189 | -4,29 | -50,440 | |
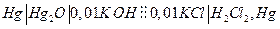
| 18,5 | 0,1636 | +3,71 | 8,37 | -3,770 |
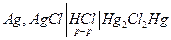
| 0,0465 | +1,27 | 3,39 | -1,050 | |

| 1,015 | -51,880 | -4,02 | -46,820 |
Очевидно, что рассчитав по таблицам термодинамических величин энергию Гиббса токообразующей реакции, можно оценить максимальную электродвижущую силу электрохимической цепи и коэффициент полезного действия, т.е. долю теплового эффекта, которая может быть превращена в электрическую энергию.
Пример.
| Токообразующая реакция | 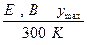
| 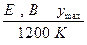
| ||
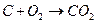
| 1,02 | 1,00 | 1,02 | 1,01 |

| 0,70 | 1,25 | 1,12 | 2,00 |
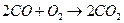
| 1,33 | 0,91 | 0,92 | 0,63 |
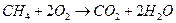
| 1,04 | 1,00 | 1,04 | 1,00 |
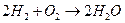
| 1,18 | 0,94 | 0,95 | 0,73 |
Очевидно, что использование электрохимического способа превращения теплоты окисления топлива в электрическую имеет несомненные преимущества перед использованием тепловых машин, где КПД в лучшем случае достигает 40 %.
19.3. Понятие электродного потенциала.
Вообще говоря, в электрохимических цепях протекают окислительно-восстановительные реакции, иначе нельзя было бы ожидать появления электронов во внешней цепи. В общей форме такую реакцию можно записать
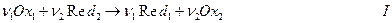
В электрохимической цепи такая реакция состоит из двух электродных процессов или двух окислительно-восстановительных полуреакций :

При этом стехиометрические коэффициенты ν1 и ν2 в реакции I соответствуют условию
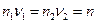
где п – число молей электронов, которое должно пройти через электрохимическую цепь, чтобы в ней осуществилась реакция I при Δλ = 1. Умножив II и III на ν1 и ν2 соответственно и вычитая одно из другого получаем реакцию I.
Комбинация относительно небольшого числа электродных полуреакций типа II и III позволяет получить множество самых различных химических реакций типа I. Комбинация N электродных полуреакций дает N(N-1)/2 химических реакций типа I.
Определим электродный потенциал как электродвижущую силу элекрохимической цепи, построенной из стандартного водородного электрода и электрода окислительно-восстановительной полуреакции. В стандартном водородном электроде плстинированный платиновый электрод погружен в раствор кислоты с активностью ионов водорода а± = 1 и омывается током водорода при давлении 1 атм (101325 Па). Электродный потенциал такого электрода принят равным нулю. К преимуществам водородного элнктрода относятся высокая точность и воспроизводимость результатов во всей области рН ( 0 ÷ 14 ), отсутствие солевой ошибки (т.е. не наблюдается изменение рН при изменении ионной силы раствора, низкое электрическое сонротивление. Однако его нельзя использовать в присутствии воздуха, кислорода, окислителей и восстановителей, кроме того платиновую чернь надо обновляь и к тому же поверхность электрода отравляется цианидами, соединениями мышьяка и сурьмы и адсорбирующимися на ней коллоидами.
Если окислитель и восстановитель электродной полуреакции находятся в стандартном состоянии, то такая эдс называется стандартным электродным потенциалом и обозначается Е0. Эти величины табулированы в справочниках физико-химических величин.
Конвенцией ИЮПАК принято считать, что эдс электрохимической цепи больше нуля, если электроны во внешней цепи движутся слева направо (и в том же направлении движутся катионы внутри электрохимической цепи)
Е > 0 → электроны во внешней цепи
→ катионы внутри цепи
← анионы внутри цепи
Е < 0 ← электроны во внешней цепи
← катионы внутри цепи
→ анионы внутри цепи
При этом заметим, что водородный электрод при измерении электродного потенциала данного электрода всегда находится слева.
Таблицы стандартных электродных потенциалов позволяют решить многие вопросы. Например, катион Mn2+ при реакции с BiO3- легко окисляется до MnO4- , который хорошо обнаруживается по фиолетовой окраске раствора. Из таблицы стандартных потенциалов имеем :
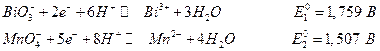
Суммарная реакция :
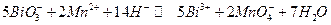
Поскольку 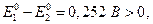 то при активностях компонентов равных единице реакция должна идти слева направо, а равновесие наступит когда потенциалы Е1 и Е2 сравняются (заметим, что п = 10) :
то при активностях компонентов равных единице реакция должна идти слева направо, а равновесие наступит когда потенциалы Е1 и Е2 сравняются (заметим, что п = 10) :
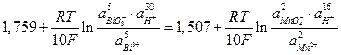
Следовательно
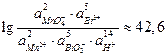
и реакция слева направо протекает количественно.
19.4. Классификация электродов.
Электродом I рода называют систему, в которой восстановленной формой является металл электрода, а окисленной формой простые или комплексные ионы этого же металла, например, система 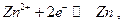 для которой
для которой
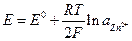
Электроды I рода обычно обратимы по катиону, т.е. их потенциал является функцией активности катиона. Существует небольшое число электродов I рода, обратимых по аниону, например,  для которого
для которого
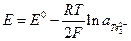
В амальгамных электродах I рода восстановленной формой служит амальгама металла, окисленной формой – ионы этого же металла
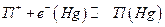
Очевидно, что для него
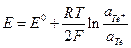
Общая формула для потенциала электрода I рода
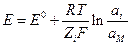
где аi – активность ионов в растворе, Zi – зарядовое число ионов в растворе с учетом знака, аМ – активность соответствующего металла (для чистого аМ = 1).
Электроды 2 рода представляют собой систему, в которой металл покрыт слоем его труднорастворимой соли (или оксида), а раствор содержит анионы этой соли (для оксида – ионы ОН- ) :
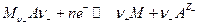
где 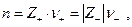 т.е. окисленной формой является труднорастворимая соль, а восстановленной – металл и анион. Если произведение активностей труднорастворимой соли
т.е. окисленной формой является труднорастворимая соль, а восстановленной – металл и анион. Если произведение активностей труднорастворимой соли 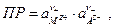 то электродный потенциал таких электродов
то электродный потенциал таких электродов

где 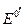 - стандартный электродный потенциал системы
- стандартный электродный потенциал системы 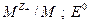 - стандартный потенциал электрода 2 рода.
- стандартный потенциал электрода 2 рода.
Примеры.
Хлорсеребряный электрод : 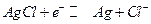

Каломельный электрод : 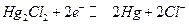
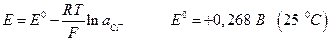
Ртутноокисный электрод : 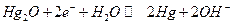
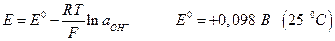
Если металл электрода не участвует в полуреакциях, а является лишь передатчиком электронов между веществами Ох и Red, то такие системы называют окислительно-восстановительными электродами или редокс – системами. Наиболее простые типа
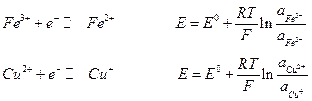
Газовые электроды тоже относятся к окислительно-восстановительным. Водородный электрод : 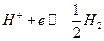
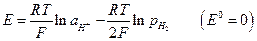
Хлорный электрод : 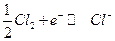
19.5. Классификация электрохимических цепей.
Их классифицируют по двум признакам : по источнику электрической энергии и по наличию или отсутствию в цепи границы двух различных растворов: соответственно цепи с переносом и без переноса (т.е. с наличием или отсутствием диффузионного потенциала).
В аллотропических цепях менее устойчивое состояние одного электрода обусловлено использованием метастабильной модификации данного материала. Например : 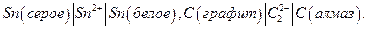 При работе цепи материал из электрода, находящегося в менее устойчивом состоянии, переходит в электрод, где он находится в более устойчивом состоянии.
При работе цепи материал из электрода, находящегося в менее устойчивом состоянии, переходит в электрод, где он находится в более устойчивом состоянии.
В концентрационных цепях оба электрода идентичны как по физическому состоянию, так и по химической природе участников редокс процессов, они отличаются только концентрацией компонентов Ох или Red. Источником электрической энергии является разность энергий Гиббса, обусловленная различными активностями одних и тех же химических компонентов.
Различают концентрационные цепи без переноса, т.е. без границы двух растворов, и с переносом, когда имеется такая граница. Цепи из двух амальгамных или двух газовых электродов с разным давлением газа содержат один раствор, и поэтому представляют собой цепи без переноса. Например, цепь
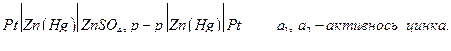
Если a1 >a2 , то электродные полуреакции :
левый электрод : 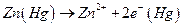
правый электрод 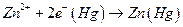
и происходит перенос цинка из амальгамы с большей активностью цинка в амальгаму с меньшей активностью. Используя условие электрохимического равновесия, можно получить, что эдс такой цепи
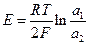
Аналогичное выражение можно получить и для газовых элекродов.
Например :
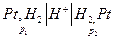
Если 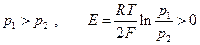 . При р2 = 1 атм и р1 >> 1, очевидно с помощью измерения эдс можно непосредственно измерить летучесь
. При р2 = 1 атм и р1 >> 1, очевидно с помощью измерения эдс можно непосредственно измерить летучесь 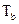 водорода (см. гл. 15 ).
водорода (см. гл. 15 ).
Но концентрационная цепь может содержать два раствора одинакового состава, но разной концентрации, и электрическая работа происходит за счет уменьшения концентрации более концентрированного раствора и увеличения концентрации более разбавленного. Очевидно, что на границе, разделяющей два раствора возникает диффузионный потенциал, что в схематической записи цепи обозначается вертикальной штриховой чертой 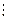 :
:
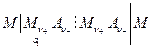
Здесь оба электрода обратимы по отношению к катионам 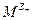 .
.
Если предположить, что концентрации двух растворов отличаются не очень сильно или оба раствора достаточно разбавлены и, следовательно, можно принять постоянство чисел переноса в переходной зоне на границе двух растворов, то для разности потенциалов на концах цепи можно получить выражение
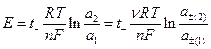
где 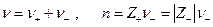
Пример. Цепь 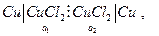 для нее
для нее 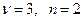 и
и
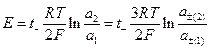
Если в растворе соли 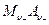 может работать не только электрод первого рода, обратимый по катионам
может работать не только электрод первого рода, обратимый по катионам 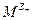 , но и электрод 2 рода, обратимый по анионам
, но и электрод 2 рода, обратимый по анионам 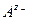 , то можно составить цепь с той же токообразующей реакцией переноса соли из концентрированного раствора в разбавленный, но без диффузионного потенциала, например :
, то можно составить цепь с той же токообразующей реакцией переноса соли из концентрированного раствора в разбавленный, но без диффузионного потенциала, например :

если а2 > а1 , то в правой части цепи идут электродные реакции

т.е. концентрация CuCl2 в растворе уменьшается, а в левой части идут обратные процессы и концентрация CuCl2 в растворе увеличивается, иными словами, электрическая работа получается за счет выравнивания концентраций растворов. Очевидно, что эдс такой цепи

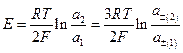
Сравнение этой эдс с эдс цепи с переносом дает возможность экспериментально определить t - .
Диффузионный потенциал при контакте достаточно разбавленных растворов электролитов можно рассчитать по приближенным уравнениям. Если контактируют растворы одного и того же электролита, но разной концентрации, то
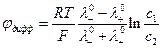
Если контактируют два разных электролита, но концентрация их одинакова ( с1 =с2 ), то
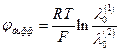
Пример.
1. Один и тот же электролит.
| c1 | c2 | φдифф , мВ | |
| HCl | 0,005 | 0,01 | +11,1 |
| 0,005 | 0,04 | +33,3 | |
| NaCl | 0,005 | 0,01 | -3,7 |
| 0,005 | 0,04 | -11,1 | |
| KCl | 0,005 | 0,01 | -0,3 |
| 0,005 | 0,04 | -1,0 |
2. Разные электролиты
| Граница | с1=с2 | φдифф , эксп | φдифф , выч |
| мВ | мВ | ||
| HCl / KCl | 0,1 | 26,8 | 28,5 |
| 0,01 | 25,7 | 27,5 | |
| HCl / NaCl | 0,1 | 33,1 | 33,4 |
| 0,01 | 33,1 | 32,0 | |
| HCl / LiCl | 0,1 | 34,9 | 36,1 |
| 0,01 | 33,8 | 34,8 | |
| KCl / LiCl | 0,1 | 8,8 | 7,6 |
| 0,01 | 8,2 | 7,1 | |
| NaCl /LiCl | 0,1 | 2,6 | 2,8 |
| 0,01 | 2,6 | 2,5 |
Легко сообразить, что если между двумя растворами, например, HCl ввести третий, например, KCl, то диффузионные потенциалы будут примерно равны по величине, но иметь разные знаки и в значительной степени взаимно уничтожат друг друга. Обычно применяют для этого растворы KCl или NH4NO3. Если диффузионный потенциал элиминирован таким солевым мостиком, то на схеме цепи такая граница обозначается двойной пунктирной чертой 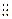 .
.
В химических цепях источником электрической энергии является энергия Гиббса химической реакции, протекающей в электрохимической системе. Такие цепи могут быть осуществлены как цепи без переноса, если один из электродов обратим по катиону, а другой – по аниону :
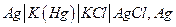
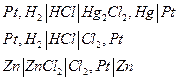
Химические цепи с переносом могут быть более разнообразны, например, элемент Даниэля – Якоби : 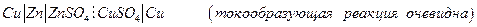
или
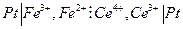
с токообразующей реакцией
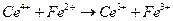
19.6. Некоторые применения измерений эдс электрохимических цепей.
Электродвижущая сила цепи без переноса

где слева электрод 1 рода, справа N электрод второго рода (обратимый по анионам AZ - ) может быть представлена в виде :
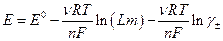
где 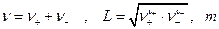 -моляльность раствора электролита.
-моляльность раствора электролита.
При заданном значении m неизвестны константа Е 0 и величина γ± . Для определения константы Е 0 строят график зависимости
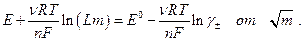
Экстраполяция прямолинейного участка зависимости (предельный закон Дебая для зависимости 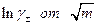 см. ранее )
см. ранее ) 
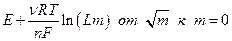 отсекает на оси ординат величину Е 0 , поскольку при
отсекает на оси ординат величину Е 0 , поскольку при 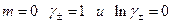 . После определения величины Е 0 по измеренной Е можно без труда рассчитать
. После определения величины Е 0 по измеренной Е можно без труда рассчитать 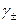 при любой заданной концентрации m .
при любой заданной концентрации m .
Произведение активностей ПР малорастворимой соли 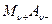 легко рассчитать по формуле
легко рассчитать по формуле
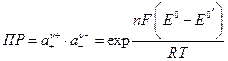 ,
,
которую легко получить из уравнения для потенциала электрода 2 рода. Здесь Е 0- стандартный потенциал 2 рода, на котором идет процесс :
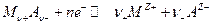
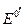 - стандартный потенциал электрода 1 рода, отвечающего равновесию :
- стандартный потенциал электрода 1 рода, отвечающего равновесию :
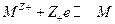 , где ион металла
, где ион металла 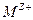 находится в той же степени окисления, что и в соли
находится в той же степени окисления, что и в соли 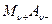 . Для электрода
. Для электрода  ,
,
для 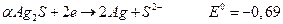
Тогда
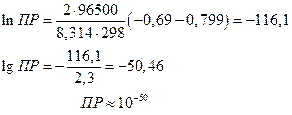
т.е. растворимость 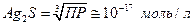
19.7. Мембранное равновесие и мембранный потенциал
Пусть имеются два раствора электролитов CA+ RA и CA которые разделены мембраной, причем ион R+ не может проникать сквозь мембрану вследствие своего большого размера. Ионы же С+ и А- и растворитель сквозь мембрану диффундируют свободно для установления электрохимического равновесия.
По условию электронейтральности растворов :

Таким образом, в растворе 1 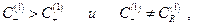 следовательно
следовательно
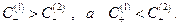 Разница в концентрациях приводит к возникновению
Разница в концентрациях приводит к возникновению
разности потенциалов между растворами (1) и (2), которая называется мембранной, которую можно зафиксировать с помощью следующей цепи :
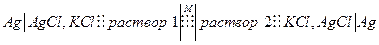
По условию электрохимического равновесия
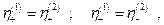 то-есть
то-есть
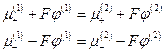
Сложение последних двух уравнений дает
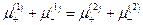 Отсюда :
Отсюда : 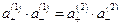 или
или
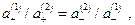 и мембранный потенциал
и мембранный потенциал
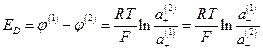
Если растворы достаточно разбавлены, то отношение активностей можно заменить отношением концентраций 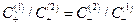 и из условий электронейтральности
и из условий электронейтральности
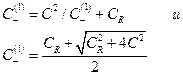
Подставив в уравнение для ED 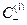 вместо
вместо 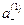 и «С» вместо
и «С» вместо 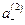 , получим
, получим
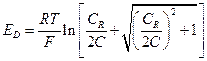
Если 
Заметим, что мембранные потенциалы нервных и мышечных волокон в состоянии покоя составляют величину 60 – 95 мВ.
Глава 20. Неравновесные электрохимические системы, основы электрохимической кинетики.
20.1. Двойной электрический слой, модельные представления.
Переход электрона из металла на находящуюся в растворе частицу или обратный процесс – переход переход электрона с частицы на электрод – протекает на границе раздела фаз и зависит от того, как построена эта граница. Поэтому знание структуры границы раздела между электродом и раствором играет большую роль при изучении кинетики и механизма электрохимических реакций. Образование двойного электрического слоя всегда тесно связано с адсорбцией на границе электрод/раствор ионов и полярных молекул, а модель двойного электрического слоя должна описывать распределение заряженных частиц и потенциала в зависимости от расстояния от поверхности электрода. На границе раздела твердое тело – электролит одни ионы преимущественно адсорбируются на поверхности твердого тела, а другие, противоположно заряженные, остаются в избытке в растворе, примыкающем к поверхности раздела.
В простейшей модели двойного электрического слоя, предложенной Гельмгольцем (1853 г.), используется модель плоского конденсатора, согласно которой к слою зарядов на металле жестко притянуты ионы противоположного знака, так что двойной слой представляет собой плоский конденсатор с очень малым расстоянием между его обкладками (порядка диаметра молекулы воды). В этой модели заряд + Q распределен по плоской поверхности площадью А и удален на расстояние d от аналогичной плоскости с зарядом -Q . Если σ = Q/A поверхностная плотность заряда, то при использовании формулы для плоского конденсатора получаем разность потенциалов двойного электрическогослоя: 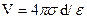
а электрическая емкость двойного слоя определяется как
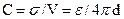
где С в Ф/см2, V в В, σ в Кл/см2.
(Электрическая емкость проводника есть отношение заряда Q проводника к его потенциалу V, т.е. C = Q/V. Единицей емкости является фарада (Ф), равная 1 Кл/В. Емкость конденсатора с параллельными пластинами дается выражением С = Аε0 ε/d (Ф), где А – площадь поверхности пластин (в м2), d – расстояние (в м), ε0 – диэлектрическая проницаемость вакуума (8,854·10-2 Ф/м), ε – относительная диэлектрическая проницаемость среды (безразмерная величина), заполняющей пространство между пластинами).
Однако, легко заметить, что принятое в модели Гельмгольца строго фиксированное расположение ионов в двойном слое в действительности невозможно, так как помимо электростатических сил на ионы действуют силы, обусловленные тепловым движением молекул. В 1910 г. Гуи и независимо от него в 1913 г Чапмен предложили теорию диффзионного слоя. В этой теории ионы рассматривались как математические точки, которые находятся под действием теплового движения и одновременно притягиваются или отталкиваются заряженной поверхностью электрода. Однако количественный расчет емкости двойного слоя по теории Гуи-Чапмена приводил к величинам, которые на несколько порядков превышали опытные значения. Это было связано с допущением теории о том, что ионы представляют собой частицы точечного размера, а поэтому могут бесконечно близко подходить к поверхности электрода.
Штерн (1924 г) учел собственные размеры ионов, предложив теорию, примерно аналогичную второму приближению теории Дебая-Гюккеля. Предполагается, что двойной электрический слой состоит из двух частей : плотного и диффузного, которые разделены плоскостью х = х2 , называемой внешней плоскостью Гельмгольца. Толщина плотного слоя примерно равна радиусу гидратированных ионов (х2 ≈ 0,3 - 0,4 нм), а его диэлектрическая постоянная значительно ниже диэлектрической постоянной в объеме раствора, что обусловлено ориентаций диполей растворителя в плотном слое как под действием электрического поля электрода, так и в результате их специфического взаимодействия с металлом. В диффузном слое напряженность электрического поля значительно меньше, а поэтому диэлектрическая постоянная приблизительно равна диэлектрической постоянной в объеме раствора. Электрические центры ионов, которые не адсорбируются специфически,доходят только до внешней поверхности Гельмгольца, а специфически адсорбирующиеся ионы входят внутрь плотного слоя, частично дегидратируясь со стороны металла. Плоскость, на которой локализуются электрические центры специфически адсорбированных ионов (х = х1), называется внутренней плоскостью Гельмгольца.
Толщина диффузного слоя теоретически бесконечна, но фактически вводят некоторую эффективную толщину, аналогичную эффективному радиусу ионной атмосферы в теории Дебая-Гюккеля. При высоких концентрациях электролита концентрация адсорбированных ионов возрастает и диффузный двойной слой сжимается, при этом его эквивалентный полный заряд оказывается ближе к поверхности электрода, таким образом, свойства границы раздела фаз приближаются к свойствам двойного слоя Гельмгольца. При очень низких концентрациях электролита диффузная часть двойного слоя начинает играть более важную роль.
20.2. Общая характеристика электрохимических процессов.
При протекании через электрохимическую цепь конечного (не бесконечно малого) тока J напряжение на концах цепи EJ не равно ее эдс, т.е. ЕJ ≠ ЕJ =0 . Если цепь работает как электрохимический источник тока, то ЕJ < ЕJ =0 , а если цепь работает как электролизер, то ЕJ > ЕJ =0, таким образом кпд при работе электрохимических систем всегда меньше 100 %.
Разность ЕJ - ЕJ =0 складывается из омического падения напряжения внутри электрохимической цепи (между катодом и анодом) Еом =JRцепи, где Rцепи<
Дата добавления: 2015-07-30; просмотров: 4141;
