Глава 17. Элементы термодинамики неравновесных систем.

17.1. Концепции.

Методы классической термодинамики (точнее, термостатики) были разработаны для описания обратимых (квазиравновесных) процессов и равновесных систем, и ее аппарат широко использует непосредственно не измеряемые термодинамические функции. Однако, возникает вопрос, в какой мере результаты классической термодинамики можно применять к неравновесным системам и к необратимо протекающим процессам. Долгое время считалось, что это невозможно, однако оказалось, что есть класс необратимых процессов, к которым можно применить термодинамические методы – это линейная термодинамика необратимых процессов, протекающих вблизи положения равновесия.

Вернемся к материалу, изложенному в гл. 4 и 5. В обратимых процессах система совершает максимально возможную работу, а при необратимом процессе работа всегда меньше. Пусть работа связана с изотермическим изменением объема системы. Обозначим через р_i давление в системе, через р_е – внешнее давление. При p_i > p_e работа, совершаемая системой над внешней средой, равна p_edV,что меньше, чем работа p_idV при обратимом расширении. Таким образом, если расширение протекает необратимо, к примеру, с конечной скоростью, то “потерянная” системой работа равна

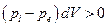
Эта величина всегда положительна независимо от того происходит ли необратимое расширение или сжатие системы:

расширение: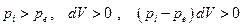

сжатие: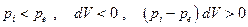

Из закона сохранения энергии следует, что энергетический эквивалент потерянной работы не может исчезнуть бесследно : он должен появиться в форме изменения энергии другого вида, и чаще всего потерянная работа переходит в теплоту. Тогда в балансе теплоты и работы при необратимом процессе следует учитывать дополнительный внутренний источник теплоты, который в реальном физическом процессе обычно проявляется в качестве теплоты трения:

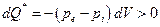
Здесь dQ^* - некомпенсированная теплота независимо от физической природы работы (механической, электрической, магнитной и т.д.).

Переход потерянной работы в теплоту – это особенность теплоты как макроскопически неупорядоченной формы передачи энергии. Если dQ_e – теплота, получаемая системой из окружающей среды, то вместо математического выражения II закона (см. гл.4)

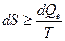
мы можем записать для баланса энтропии системы следующее соотношение

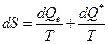
Заметим, что всегда 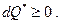Очевидно, что (см. § 5.1) вообще говоря

,

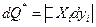где X_i и y_i – обобщенная сила и обобщенная координата любого вида работы. Например, при необратимом переносе электрического заряда под действием разности электрических потенциалов в качестве dQ^* выступает джоулево тепло.

Заметим еще раз, что энтропия системы как функция состояния не зависит от способа достижения этого состояния (обратимо или необратимо), другое дело как вычислить изменение энтропии. Если dS – общее изменение энтропии системы, то теплота dQ_e отвечает не полному количеству теплоты, полученному системой, а только теплоте, взятой из окружающей среды. Для изолированной системы dQ_e = 0, и следовательно

17.2. Термодинамический анализ необратимых процессов.

Для этого необходимо получить ответы на следующие проблемы.

1. Является ли в этом случае допустимым использовать термодинамические соотношения для энтропии и других связанных с нею термодинамических функций.

2. Какой смысл имеет величина 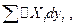неизбежно входящая в уравнение баланса энергии.

3. При наличии разности обобщенных сил ΔХ_i ≠ 0, процессы переноса по обобщенным координатам y_i протекают с конечными скоростями. Как связаны скорости (потоки) по данной координате с вызывающими их разностями обобщенных сил ΔХ_i.

Для решения этих проблем необходимо ввести ряд дополнительных постулатов, которые не являются общими законами природы, поэтому могут существовать (и существуют) необратимые процессы, для которых развиваемая ниже теория неприменима (или практически бесполезна).

В качестве первого постулата вводится предположение о локальном равновесии во всех частях рассматриваемой системы, согласно которому такую систему можно представить в виде совокупности макроскопических, но малыхэлементов объема, к каждому из которых допустимо применять обычные термодинамические методы – указать локальные температуру, давление, вычислить энтропию и т.п., что позволяет задать для неравновесной системы поле интенсивных термодинамических параметров (обобщенных сил), в результате чего в этих полях будут наблюдаться потоки соответствующих им координат состояний, к которым можно применить дифференциальные уравнения переноса. Однако этот постулат не выполняется для сильно неоднородных систем, когда происходит заметное изменение термодинамических параметров на расстояниях порядка длины свободного пробега молекул, или при больших отклонениях от закона равновесного распределения частиц по энергии.

Второй постулат состоит в предположении, что вся потерянная работа полностью переходит в теплоту

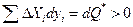
Для построения аппарата термодинамики необратимых процессов необходимо выразить dQ^* через измеряемые экспериментально величины. Введем в рассмотрение потоки I_k, определяемые как

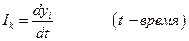
Скорости процессов связаны, вообще говоря, не с разностями ΔХ_i, а с градиентом величины Х_i, обозначим их

,

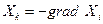где Х_к в термодинамике необратимых процессов называется силой, а знак минус в правой части равенства означает только то, что положительное направление координатной оси при вычислении градиента всегда выбирают в сторону уменьшения Х_i, благодаря чему силы Х_к всегда положительны.

Поток некомпенсированной теплоты обусловлен наличием в системе градиентов Х_i и потоков I_k, т.е. постоянным переходом работы в теплоту

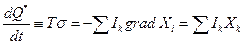
где 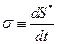представляет собой локальное возникновение (возрастание) энтропии в результате протекания необратимых процессов. Важно то, что величину σ можно однозначно связать со значениями термодинамических функций состояния в каждой точке неравновесной системы.

Здесь возникают два обстоятельства. В вышеприведенном уравнении баланса “некомпенсированной теплоты” и “потерянной работы” абсолютные величины потоков I_k и "сил" X_k можно определять различным образом при сохранении общего условия баланса. Далее потоки I_k представляют собой явные функции сил X_k, следовательно необходимо иметь вид кинетических уравнений

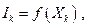
простейшими из которых являются линейные уравнения, связывающие потоки и силы. Простейшими с математической точки зрения являются линейные соотношения типа 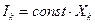, когда поток I_k пропорционален величине вызвавшей его “силы” 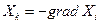. Действительно, согласно закону Фурье поток теплоты через поверхность Ω

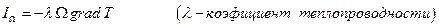
Согласно закону Ома поток заряда

(ρ – электрическая проводимость, φ – электрический потенциал).

Закон диффузии Фика 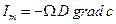легко преобразовать к выражению, содержащему градиент химического потенциала. Действительно, диффузионный поток через поверхность Ω пропорционален подвижности частиц (D^΄) стартовой концентрации вещества «с» у поверхности Ώ к градиенту химического потенциала:

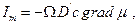
а так как для идеальных растворов

,

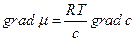то получаем закон Фика , если величины D и D^΄ связаны соотношением

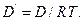
Феноменологические уравнения переноса (Фурье, Ома, Фика) получены в физике независимо от термодинамики и вычисление соответствующих им σ_Q, σ_e или σ_m сравнительно мало интересно.

Существенно более важные результаты в теории явлений переноса могут быть получены при описании более сложных явлений потоков теплоты, заряда или массы в полях нескольких одновременно действующих сил, например, при одновременном наличии градиентов температуры, электрического потенциала и химического потенциала. Эти явления называют перекрестными явлениями переноса, например, термоэлектрические явления, эффекты термодиффузии и т.п., которых известно несколько десятков.

При небольших отклонениях от равновесия (незначительная величина сил Х_к) поток I_i есть в общем случае линейная функция всех сил X_k :

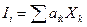
Очевидно для действующих двух сил X_i и X_k имеем два потока I_i и I_k, для которых

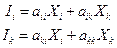
В 1931 г. Онзагеру удалось показать, что для сложных процессов переноса справедливо :

a_ik = a_ki

Это соотношение выражает важнейший результат линейной термодинамики необратимых процессов переноса – соотношение взаимности Онзагера. При его статистическом выводе использован принцип микроскопической обратимости (в применении к химическому процессу этот принцип есть известное для химика утверждение, что в равновесной смеси все частные реакции протекают в обоих направлениях с одинаковой скоростью) и допущение о том, что затухание флуктуаций можно описывать линейными уравнениями макроскопической физики.

Соотношения Онзагера не просто сокращают вдвое число параметров в кинетических уравнениях переноса, но с их помощью удалось построить полную макроскопическую теорию перекрестных явлений переноса.

В итоге методы линейной термодинамики необратимых процессовмогут быть использованы при следующих условиях :

1. в системе устанавливается локальное равновесие, что позволяет использовать для описания свойств системы обычные термодинамические переменные и вводить макроскопические параметры для описания кинетики процессов;

2. наблюдается полный переход «потерянной работы» в теплоту, что позволяет составить точное уравнение баланса энтропии и одновременно использовать другие уравнения баланса макроскопических величин;

3. соблюдаются линейные кинетические законы, связывающие потоки и силы. Это дает отсутствующие в термодинамике сведения о скоростях изменения термодинамических параметров неравновесной системы;

4. можно использовать соотношения взаимности Онзагера.

Если неравновесная система находится в стационарном состоянии, то оказывается справедливой теорема Пригожина : если система удовлетворяет четырем вышеуказанным требованиям термодинамики необратимых процессов, если все коэффициенты a_ik в линейных кинетических уравнениях постоянны, то при поддержании постоянных значений обобщенных сил на границах системы в стационарном состоянии возникновение энтропии σ оказывается минимальным.

Таким образом, стационарному состоянию неравновесной системы при заданных условиях сопряжения системы со средой удается сопоставить экстремум функции σ точно так же, как для равновесной системы экстремумы характеристических функций.

В 1958 году Ларсу Онзагеру была присуждена Нобелевская премия по химии за формулировку соотношений взаимности, имеющая важное значение для термодинамики необратимых процессов.

В 1977 году Илье Пригожину была присуждена Нобелевская премия по химии за вклад в термодинамику необратимых процессов, особенно в теорию диссипаривных систем.