Определнный интеграл, его геометрический смысл, свойства.
Определённый интеграл — аддитивный монотонный нормированный функционал(???!!!), заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).
Пусть f(x) определена на [a;b]. Разобьём [a;b]на части с несколькими произвольными точками a = x0 < x1 < x2 < xn = b Тогда говорят, что произведено разбиение RR отрезка [a;b] Далее выберем произв. точку 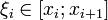 , i = 0, Определённым интегралом от функции f(x) на отрезке [a;b]называется предел интегральных сумм ΘR при
, i = 0, Определённым интегралом от функции f(x) на отрезке [a;b]называется предел интегральных сумм ΘR при 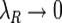 , если он существует независимо от разбиения R и выбора точек ξi, т.е.
, если он существует независимо от разбиения R и выбора точек ξi, т.е. 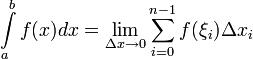 (1) Если существует (1), то функция f(x) называется интегрируемой на [a;b] – определение интеграла по Риману.
(1) Если существует (1), то функция f(x) называется интегрируемой на [a;b] – определение интеграла по Риману.
a – нижний предел. b – верхний предел. f(x) – подынтегральная функция. λR - длина частичного отрезка. σR – интегральная сумма от функции f(x) на [a;b] соответствующей разбиению R. λR - максимальная длина част. отрезка.
Дата добавления: 2015-07-24; просмотров: 715;
