Свойства верхней и нижней граней множества
1о. Если a* = sup X, то
1) 
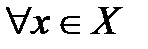выполняется неравенство 
.
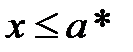2) 
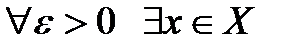такое, что выполняется неравенство 
.
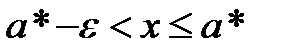2о. Если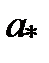 
= inf X то
1) 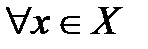выполняется неравенство 
.
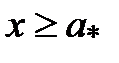2) 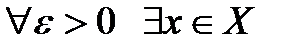такое, что выполняется неравенство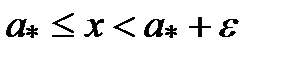 
Теорема 5.1.Всякое ограниченное сверху (снизу) множество имеет верхнюю (нижнюю) грань и при том только одну.
Дано.
Доказать.
Доказательство.
Замечание 5.1. Если множество Х неограниченно сверху (снизу), то будем считать sup X =+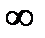 
(inf X =– 
).
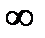В заключение приведем
Аксиому Архимеда.Каким бы ни было действительное число k, всегда есть натуральное число n, которое больше k.
Из этой аксиомы следует, что множество натуральных чисел неограниченно.
Пример 5.2.Найти верхнюю и нижнюю грани множеств:
Дата добавления: 2015-07-24; просмотров: 831;