П.2. Способы задания функции.
1. Аналитический, т. е. с помощью формулы. Если функция задана формулой и не дано дополнительных ограничений, то областью определения функции считают множество всех значений переменной, при которых эта формула имеет смысл. Иногда функция задается в области определения не одной формулой, а несколькими разными формулами. Пример 6.1.Функция
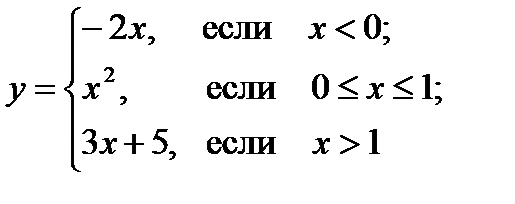
задана аналитическим способом на множестве действительных чисел при помощи трех разных формул.
Пример 6.2. Функция Дирихле
Пример 6.3. y=sgn x
2. Табличный способ.
3. Словесный (описывают словами закон, по которому находятся значения функции).
Пример 6.4. Функция f каждому квадрату со стороной а ставит в соответствие его площадь.S(a)=a2, a>0.
Пример 6.5. Каждому действительному числу х поставим в соответствие наибольшее целое число, которое не превосходит y. Эта функция – Антье, обозначается E(x)=[x], её график.
4. Графами.
5. Графический (только для числовых функций числового аргумента).
Определение 6.4. Графиком функции 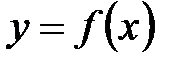 , заданной на множестве Х, называется множество всех точек плоскости с координатами
, заданной на множестве Х, называется множество всех точек плоскости с координатами 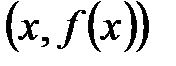 , где х Î D(f).
, где х Î D(f).
Заметим, для того чтобы некоторое множество точек плоскости являлось графиком какой–либо функции, необходимо, чтобы это множество имело не более одной общей точки с любой прямой, параллельной оси Оу.
Рис. 10 Рис. 11
Дата добавления: 2015-07-24; просмотров: 1336;
