Квадратичная функция.

Степенная функция. Область определения степенной функции 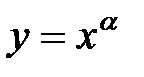зависит от показателя a. Эта функция при любом a определена в интервале 0 < х < +¥, то есть для всех положительных значений х. При a натуральном областью определения является вся числовая ось. Множеством значений функции будет интервал 0 < у < +¥ при a четном и промежуток –¥ < у < +¥ при a нечетном (рис. 15).

Рис. 15

Показательная функция. Областью определения показательной функции 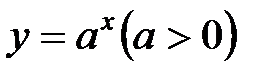является вся числовая ось, то есть промежуток (–¥; + ¥), а множеством значений функции - промежуток (0; + ¥) (рис. 16).

Рис. 16

Логарифмическая функция. Областью определения логарифмической функции 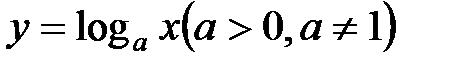является промежуток 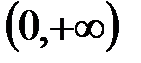, а множеством значений функции - промежуток 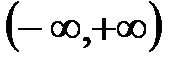(рис. 17).

Рис. 17

Тригонометрические функции. Областью определения функций y = sinx и y = cosx является промежуток 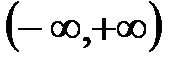, а множеством значений функций –– отрезок [–1; 1] (рис. 18 и 19).

Рис. 18 Рис. 19

Функция 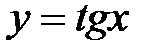определена на всей числовой оси, кроме точек 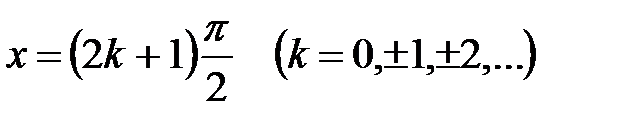, т.е. область определения этой функции есть совокупность интервалов

.

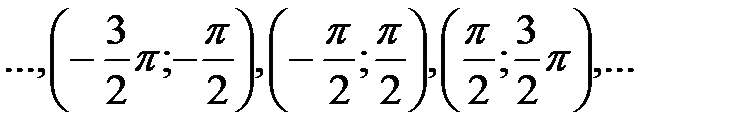Функция 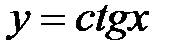определена на всей числовой оси, кроме точек 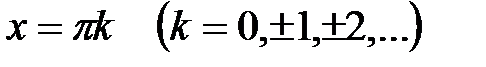, т.е. область определения этой функции состоит из интервалов

.

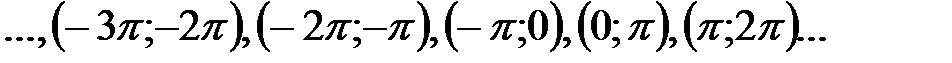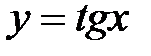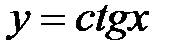Множеством значений функций и является промежуток 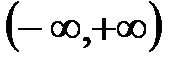(рис. 20 и 21).

Рис. 20 Рис. 21

Обратные тригонометрические функции. Областью определения функций y = arcsinx и

y = arccosx является отрезок [– 1; 1]. Множеством значений функции y = arcsinx является отрезок 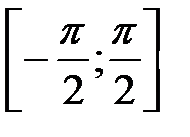, а функции y = arccosx –– отрезок 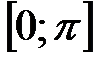(рис. 22 и 23).

Рис. 22 Рис. 23

Областью определения функций y = arctgx и y = arcсtgx является промежуток 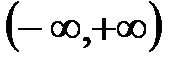. Множеством значений функции y = arctgx будет интервал 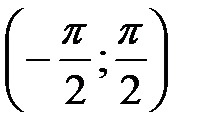, а функции y = arcсtgx –– интервал 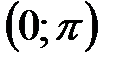(рис. 24 и 25).

Рис. 24 Рис. 25