П.5. Обратная функция

Определение 6.11. Пусть функция 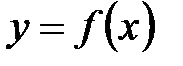определена и возрастает (убывает) на промежутке Х, а область значений функции есть промежуток Y. Каждому значению у₀ из промежутка Y будет соответствовать одно значение х₀ Î Х такое, что 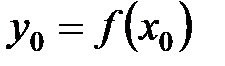(рис. 13). Следовательно, на промежутке Y определена функция 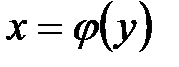. Функция 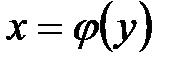называется обратной для функции 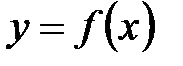и, наоборот, функция 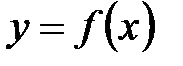является обратной для функции .

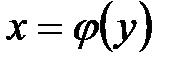Рис. 13

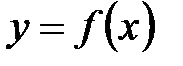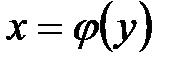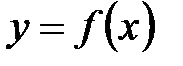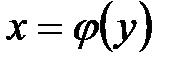Переход от функции к обратной функции сводится только к изменению роли множеств Х и Y. Поэтому графики функций и (как множества точек плоскости хОу) совпадают. Однако обычно и для обратной функции аргумент обозначают через х, а значения функции –– через у, то есть вместо 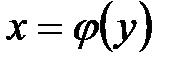пишут 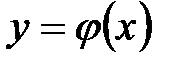. Графики функции 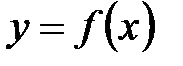и обратной функции 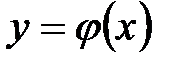в этом случае будут симметричны относительно прямой у = х (рис. 14).

Рис. 14