Волновая функция. Уравнение Шрёдингера.
Если частицы обладают волновыми свойствами, то можно говорить не только о длине волны, присущей данной частице, но и об амплитуде этой волны, и о её интенсивности, т.е. частица должна быть некоторым образом размазана по пространству, и в какой-то области пространства её должно быть больше, а в какой – то меньше.
Наличие максимумов и минимумов в опыте Девисона и Джемера было связано с большей и меньшей интенсивностью волн, присущих отраженным электронам. Следовательно, интенсивность волн де Бройля в данной области пространства определяет число частиц, попавших в эту область. Согласно М.Планку, интенсивность волн де Бройля является мерой вероятности того, что частицы находятся в данной области пространства. Для определения вероятности нахождения частицы в данном объеме пространства 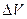 была введена некоторая функция
была введена некоторая функция 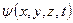 – волновая функция или пси-функция. Она выбирается такой, чтобы вероятность
– волновая функция или пси-функция. Она выбирается такой, чтобы вероятность 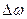 нахождения микрочастиц в объеме
нахождения микрочастиц в объеме 
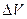 была пропорциональна квадрату модуля пси-функции и элементу этого объема:
была пропорциональна квадрату модуля пси-функции и элементу этого объема:
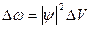 . (3)
. (3)
Тогда отношение 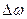 к величине объема
к величине объема 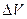 есть плотность вероятности нахождения частицы.
есть плотность вероятности нахождения частицы.
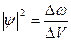 –плотность вероятности нахождения частицы в данной области пространства.
–плотность вероятности нахождения частицы в данной области пространства.
Т.к. эта частица где – то в пространстве имеется, 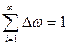 или
или 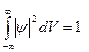 - условие нормировки
- условие нормировки 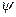 - функции.
- функции.
Условие нормировки утверждает объективность существования частицы в пространстве.
Волновая 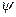 - функция является основной характеристикой состояния микрообъектов в квантовой механике. Она не позволяет однозначно определять положение частицы в пространстве, а дает лишь возможность найти вероятность обнаружения частицы в данной области пространства.
- функция является основной характеристикой состояния микрообъектов в квантовой механике. Она не позволяет однозначно определять положение частицы в пространстве, а дает лишь возможность найти вероятность обнаружения частицы в данной области пространства.
Согласно М. Борну (1926г.), квадрат модуля 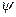 - функции определяет вероятность того, что частица будет обнаружена в пределах объема
- функции определяет вероятность того, что частица будет обнаружена в пределах объема 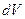 .
.
Уравнение Шрёдингера.
Наличие у микрочастиц волновых свойств делает невозможным применение в квантовой механике законов классической физики, в частности, законов Ньютона.
Необходимо было записать уравнение, с помощью которого, зная начальные условия, можно было бы рассчитать параметры волн де Бойля и вероятность нахождения частицы в любой момент времени. Такое уравнение было записано швейцарским физиком Шредингером в 1926г. Оно не выводилось теоретически, а постулировалось. Подтверждением его правильности явилось то, что все вытекающие из него следствия подтверждались опытными фактами. Для частицы, находящейся в стационарном силовом поле (электрическом, гравитационном) оно имеет вид:
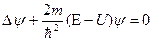 , (4)
, (4)
где 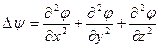 –оператор Лапласа,
–оператор Лапласа,
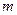 –масса частицы,
–масса частицы,
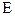 –полная энергия частицы,
–полная энергия частицы,
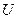 –потенциальная энергия частицы силовом поле.
–потенциальная энергия частицы силовом поле.
В этом случае 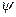 не зависит от
не зависит от 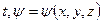 (т.к. поле стационарно).
(т.к. поле стационарно).
Уравнение (4) применимо для частиц, скорости которых малы по сравнению со скоростью света; для больших скоростей имеется более точное уравнение Дирака.
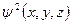 –плотность вероятности нахождения частиц в окрестностях интересующей нас точки с координатами
–плотность вероятности нахождения частиц в окрестностях интересующей нас точки с координатами 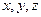 .
.
Согласно (3), вероятность нахождения частицы в определенной точке 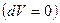 равна нулю, т.е. в квантовой физике имеет смысл определять вероятность нахождения частицы только в некоторой, не равной нулю, области пространства.
равна нулю, т.е. в квантовой физике имеет смысл определять вероятность нахождения частицы только в некоторой, не равной нулю, области пространства.
Из смысла 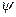 - функции вытекает, что квантовая механика имеет статистический характер. Она не позволяет определить местонахождение частицы в пространстве или траекторию частицы, а может лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. В применении к микрочастицам понятие определенного местоположения и траектории вообще теряет смысл.
- функции вытекает, что квантовая механика имеет статистический характер. Она не позволяет определить местонахождение частицы в пространстве или траекторию частицы, а может лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. В применении к микрочастицам понятие определенного местоположения и траектории вообще теряет смысл.
 Рассмотрим решение уравнения Шрёдингера для случая, когда частица находится в "потенциальной яме" шириной
Рассмотрим решение уравнения Шрёдингера для случая, когда частица находится в "потенциальной яме" шириной 
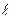 с потенциальными плоскими вертикальными "стенками". В этом случае она может двигаться только вдоль оси
с потенциальными плоскими вертикальными "стенками". В этом случае она может двигаться только вдоль оси 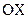 между точками с координатой
между точками с координатой 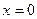
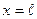 (рис. 4) и в этих пределах потенциальная энергия силового поля равна нулю, а как только частица выходит за указанные пределы, потенциальная энергия поля становится бесконечно велика и поле моментально "загонит" частицу обратно, вернее, оно просто не даст частице выскочить за пределы "ямы".
(рис. 4) и в этих пределах потенциальная энергия силового поля равна нулю, а как только частица выходит за указанные пределы, потенциальная энергия поля становится бесконечно велика и поле моментально "загонит" частицу обратно, вернее, оно просто не даст частице выскочить за пределы "ямы".
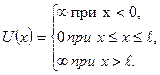
По условию задачи (бесконечно высокие "стенки"), частица не проникает за пределы  "ямы", поэтому вероятность её обнаружения (а следовательно, и волновая функция) за пределами
"ямы", поэтому вероятность её обнаружения (а следовательно, и волновая функция) за пределами  "ямы" равна нулю. На границах
"ямы" равна нулю. На границах  "ямы" (при
"ямы" (при 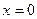 ,
, 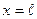 ) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид
) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид
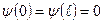 .
.
В пределах  "ямы" (
"ямы" ( 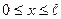 ) уравнение Шредингера сведется к уравнению
) уравнение Шредингера сведется к уравнению
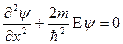 .
.
Обозначим 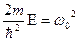 .
.
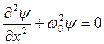 ,
,

Т.к. 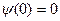 ,
, 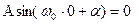 , т.е.
, т.е. 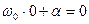
 ,
, 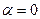 .
.
Т.к. 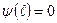 ,
, 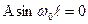 ,
,  , т.е.
, т.е. 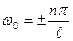 ,
,
 ,
, 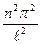 =
= 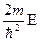 ,
, 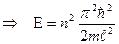 (n=1,2,3,….),
(n=1,2,3,….),
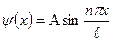 .
.
Таким образом, частица в такой "потенциальной яме" может иметь лишь дискретный набор значений энергии – спектр энергии (рис. 5).

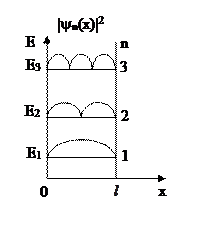
|
Дата добавления: 2015-08-08; просмотров: 2726;
