Соотношение неопределенностей Гейзенберга.

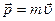Микрочастицы, особенно такие легкие как электрон, ведут себя, в зависимости от условий, то почти так же как "настоящие" частицы, то совсем иначе. Если при движении частицы её импульс не меняется или меняется медленно, то микрочастица ведёт себя почти так же, как классическая частица. Но если импульс меняется быстро (при движении электрона вокруг ядра по орбите малого радиуса, когда импульс быстро меняет своё направление), микрочастица ведет себя совершенно иначе чем обычные частицы, скорее как волна. Говорят, что микрочастицы обладают волновыми свойствами.

Волновые свойства микрочастицы выражены сильнее или слабее в зависимости от быстроты изменения импульса. Чем быстрее меняется импульс, тем сильнее выражены волновые свойства микрочастицы. Можно ли предсказать, а когда волны и микрочастицы будут вести себя подобно макрочастицам (т.е. проявляются корпускулярные свойства) и когда их поведение будет качественно другим? Оказывается, это возможно. Микрочастицы будут двигаться в данном направлении подобно обычным большим частицам, если их движение в этом направлении не определяется большими действующими силами или не стеснено узкими рамками.

Если свет проходит через щель, ширина которой велика по сравнению с длиной волны 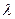(рис. 2), его поведение подобно поведению классических частиц (корпускул). Если уменьшить ширину щели, то при 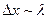волны начнут распространяться не только в первоначальном, но и в других направлениях, огибая края щели (дифракция).

Аналогично для микрочастиц: чем уже щель, тем сильнее ограничение движению частиц, и как бы протестуя против этого, микрочастицы огибают края щели, приобретая разнообразные импульсы в направлении 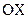(рис. 3).

До щели импульс частиц в направлении 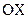равнялся нулю, т.е. был строго определенным. После щели импульс в направлении 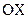для разных микрочастиц различен. Обозначим неопределенность (максимальный разброс) в импульсе вдоль оси 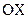через 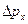, а импульс до прохождения через щель р. Чем больше отношение 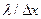, тем больше возможное отклонение микрочастицы от первоначального направления, т.е. тем больше отношение .

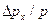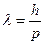; т.к. , то .

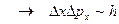Это знаменитое соотношение неопределенностей, принадлежащее одному из основателей квантовой механики В. Гейзенбергу (1927г.). Его смысл – реакция частицы на локализацию, т.е. на ограничение её пространственного движения. Чем меньше область , в которой вынуждена двигаться частица, тем больше у неё неопределенность в импульсе 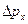.Можно теоретически доказать (Г. Вейль), что наименьшим возможным является произведение флуктуаций

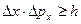. (1)

Принцип неопределенности Гейзенберга: волновая природа микрочастиц приводит к тому, что микрочастица не может иметь одновременно определенную координату 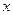и компоненту импульса . Неопределенности значени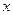й и удовлетворяют соотношению (1).

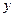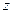Аналогичные соотношения имеют место для и , и 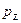.Таким образом, Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения в их поведении, пришел к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой, и импульсом. Согласно соотношению неопределенностей Гейзенберга, микрочастица не может иметь одновременно и определенную координату 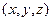и определенную собственную проекцию импульса 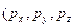), причем неопределенности этих величин удовлетворяют условиям

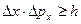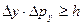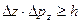, , . (2)

Т.е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

В квантовой теории рассматривается также соотношение неопределенностей для энергии 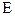и времени t, т.е. неопределенность этих величин удовлетворяет условию

.

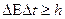Если длительность пребывания частицы в данном состоянии рана 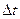, то неопределенность энергии частицы в этом состоянии составляет .

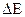Соотношение неопределенностей является одним из фундаментальных положений квантовой механики.

Рассмотрим, к каким результатам приводят эти соотношения. Если велико по сравнению с атомными размерами (т.е. с 10^-10м), то ограничения на движение частицы, накладываемые соотношением (1), не является существенными.

Пусть для пылинки с координата определена с точностью .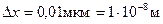

, , , .

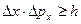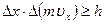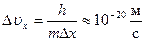Такая неопределенность не играет никакой роли при любых скоростях, т.е. можно считать, что такое макроскопическое тело имеет одновременно определенное значение 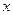и .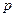

Для электрона в атоме в наиболее грубом случае координату можно определить с точностью до размеров атома, т.е. .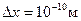

.

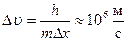Но такую же по порядку величину имеет и сама скорость электрона в атоме, 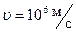. Следовательно, скорость электрона имеет значение в интервале , , 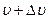т.е. от 0 до 2·10⁶м/с, т.е. оказывается совершенно неопределенной (а, следовательно, и импульс не определен).