Поняття про зони Бріллюена

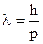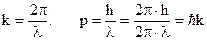Згідно з гіпотезою де Бройля електрон має хвильові властивості з довжиною хвилі , де h – стала Планка, р = mυ – імпульс. Кінетична енергія . Імпульс можна виразити через хвильове число . Тоді кінетична енергія буде 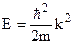. (4.1)

Ця залежність енергії від хвильового числа називається дисперсійною кривою. Для вільного електрона вона уявляє квадратну параболу.

Якщо вільний електрон рухається в кристалі, на нього діє періодичне поле атомів. Розв’язуючи рівняння Шредінгера для електрона, який рухається в періодичному полі, вимога нерозривності хвильової функції та її перших похідних приводить до того, що дисперсійна крива Е(k) (рис.4.4) зазнає розривів при значеннях хвильових чисел k = ±n×π/a, де n = 1, 2,3…, а – період поля (стала кристалічної гратки).

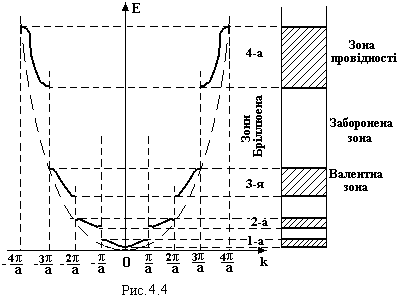Пунктиром показана дисперсійна крива вільного електрона, суцільною – електрона в кристалі. Інтервали значень хвильового числа k, в межах яких енергія змінюється неперервно, а на границях зазнає розриву, називаються зонами Бріллюена. 1-а зона простирається від –π/а до +π/а, 2-а від -2π/а до -π/а і від + π/а до +2 π/а і т.д. На рис.4.4 показані дисперсійні криві і зони Бріллюена для лінійного одноатомного ланцюга. У трьохмірному випадку зони Бріллюена уявляють собою досить складні замкнуті поверхні - багатогранники, вставлені один в один. Їх називають дисперсійними поверхнями

Відмітимо загальні властивості границь зон Бріллюена і зон дозволених значень енергії:

а) Дно зони дозволених значень енергії відповідає мінімуму дисперсійних поверхонь (зон Бріллюена);

б) Стеля зони дозволених значень енергії відповідає максимуму дисперсійних поверхонь (зон Бріллюена).

в) В межах зони Бріллюена між мінімумом і максимумом завжди є точка перегину.