Теплове розширення твердих тіл

Зміна геометричних розмірів твердих тіл при зміні температури називається тепловим розширенням. Для пояснення природи цього явища розглянемо залежність потенціальної енергії U взаємодії між атомами від відстані r між ними (рис. 3.4, суцільна крива 2). Вона відображає крайні положення r₁ і r₂ частинки, яка здійснює ангармонічні (негармонічні) коливання відносно положення рівноваги r_o при температурі відмінній від 0К. Ця крива асиметрична відносно лінії . 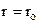Ліва вітка іде крутіше, ніж права. Тому відхилення частинки вліво 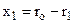менше, ніж вправо 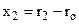. Середня відстань 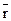(точка А) більша від рівноважної . А це й означає розширення кристалу. У випадку протилежної аси 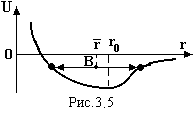метрії кривої потенціальної енергії (рис.3.5) кристал з ростом температури буде стискуватись.

Для кількісного описання явища теплового розширення лінійного наближення залежності сили F взаємодії від зміщення 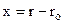, яке приймається в законі Гука, в теорії теплоємності, тепер уже недостатньо. Дійсно, в лінійному наближенні сила 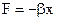, а потенціальна енергія

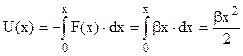(3.15)

уявляє собою квадратну параболу (рис. 3.4, крива 1), симетричну відносно положення рівноваги. Тому середня відстань не змінюється. Отже, в ряді розкладення сили по степеням х враховується і квадратичний член з коефіцієнтом ангармонічності g

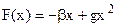. (3.16)

Потенціальна енергія, яка знаходиться аналогічно (3.15),

(3.17)

описує асиметричну криву 2 рис. 3.4. Дійсно, знак другого доданку (3.17) змінюється у відповідності із знаком х. При відхиленні вліво x<0 і графік іде вище квадратної параболи, при відхиленні вправо x>0 і крива іде нижче параболи.

Знайдемо коефіцієнт α теплового розширення, як відносну зміну геометричного розміру при зміні температури на 1К

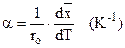. (3.18)

Середнє зміщення 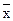знаходимо усереднивши силу у виразі (3.16). Ясно, що середнє значення сили дорівнює нулю

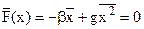. (3.19)

Середнє значення потенціальної енергії дорівнює половині повної енергії гратки, тобто

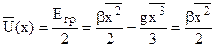. (3.20)

Тут враховано, що середнє значення 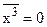, так як в процесі коливань х змінює знак. Із (3.20) знаходимо 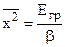, підставляємо в (3.19). Одержуємо 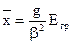. Тоді із (3.18) маємо

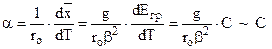. (3.21)

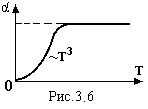
Отже температурна залежність коефіцієнта теплового розширення аналогічна рис.3.1 температурній залежності теплоємності гратки. Для більшості металів коефіцієнт теплового розширення знаходиться в межах

10^-4 ÷ 10^-5 К^-1.