Физика атома и атомного ядра. Пример 1.Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность по-тенциалов U
Пример 1.Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность по-тенциалов U. Найти длину волны де Бройля  , если: 1) U1 = 51 В; 2) U2 = 510 кВ.
, если: 1) U1 = 51 В; 2) U2 = 510 кВ.
Решение. Длина волны де Бройля частицы зависит от ее импульса р и рассчитывается по формуле
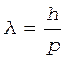 , (1)
, (1)
где h - постоянная Планка.
Импульс частицы можно определить, если известна ее кинетическая энергия 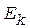 . Связь импульса с кинетической энергией различна для нереляти-вистского случая (когда кинетическая энергия частицы много меньше ее энергии покоя) и для релятивистского случая (когда они сравнимы между собой).
. Связь импульса с кинетической энергией различна для нереляти-вистского случая (когда кинетическая энергия частицы много меньше ее энергии покоя) и для релятивистского случая (когда они сравнимы между собой).
В нерелятивистском случае
 , (2)
, (2)
где  - масса покоя частицы.
- масса покоя частицы.
В релятивистском случае
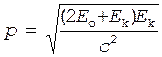 , (3)
, (3)
где 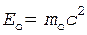 - энергия покоя частицы.
- энергия покоя частицы.
В нерелятивистском случае из формулы (1) и соот-ношения (2) следует:
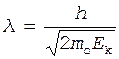 . (4)
. (4)
В релятивистском случае из формулы (1) и соот-ношения (3) следует:
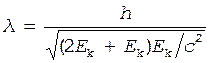 . (5)
. (5)
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U1 = 51 В и U2 = 510 кВ, с энергией покоя электрона Ео = moc2 = 0,51 МэВ и в зависимости от этого решим, какую из только что полученных формул следует применить для вычисления длины волны де Бройля.
Как известно, кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, равна Ek = еU.
В первом случае  МэВ, что много меньше энергии покоя электрона. Следовательно, для вычисления
МэВ, что много меньше энергии покоя электрона. Следовательно, для вычисления  можно применить формулу (4). Для упрощения расчетов заметим, что
можно применить формулу (4). Для упрощения расчетов заметим, что  Подставив это выражение в формулу (4), перепишем ее в виде
Подставив это выражение в формулу (4), перепишем ее в виде
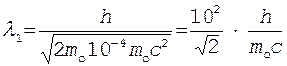 .
.
Учитывая, что  есть комптоновская длина волны
есть комптоновская длина волны 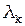 , получаем
, получаем
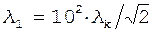 .
.
Подставив сюда значение  пм, находим
пм, находим
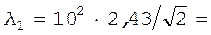 155 пм.
155 пм.
Во втором случае кинетическая энергия 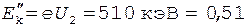 МэВ, т.е. равна энергии по-коя электрона. Для вычисления
МэВ, т.е. равна энергии по-коя электрона. Для вычисления 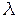 необходимо при-менить формулу (5):
необходимо при-менить формулу (5):
 1,27 пм.
1,27 пм.
Пример 2.Кинетическая энергия электрона в атоме водорода составляет величину порядка 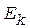 =10 эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома.
=10 эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома.
Решение. Соотношение неопределенностей для координаты и импульса имеет вид
Dx×Dp ³  , (1)
, (1)
где Dх - неопределенность координаты частицы (в данном случае электрона);
Dр - неопределенность импульса электрона;
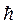 - постоянная Планка (h/2p).
- постоянная Планка (h/2p).
Из соотношения неопределенностей следует, что, чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с
неопределенностью
Dх = l/2.
Соотношение неопределенностей (1) можно записать в этом случае в виде
(l/2)Dр ³ 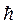 ,
,
откуда
l ³  /Dp.
/Dp.
Неопределенность импульса не должна превышать значение самого импульса р, т.е. Dр £ р. Импульс р связан с кинетической энергией соотношением 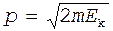 . Заменим Dр значением
. Заменим Dр значением 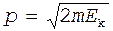 . (Такая замена не увеличит величину l.) Переходя от неравенства к равенству, получим
. (Такая замена не увеличит величину l.) Переходя от неравенства к равенству, получим
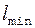 =
=  /
/  . (2)
. (2)
Проверим размерность 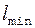 . Для этого в правую часть формулы (2) вместо символов величин подставим их единицы измерения:
. Для этого в правую часть формулы (2) вместо символов величин подставим их единицы измерения:
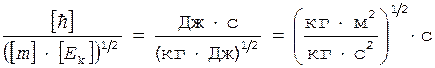 = м.
= м.
Найденная единица измерения является единицей измерения длины.
Произведем вычисления:
 м.
м.
Пример 3.Волновая функция  описывает состояние частицы в бесконечно глубокой потенциальной яме шириной l. Вычислить вероятность
описывает состояние частицы в бесконечно глубокой потенциальной яме шириной l. Вычислить вероятность
нахождения частицы в малом интервале Dl, состав-ляющем 1% от ширины ямы, в двух случаях:
1) вблизи стенки (0 £ х £ Dl);
2) в средней части ямы (l/2 - Dl/2 £ х £ l/2 + Dl/2).
Решение. Вероятность того, что частица будет обнаружена в интервале dx (от x до x + dx), пропорциональна этому интервалу и квадрату модуля волновой функции, описывающей данное состояние:
 .
.
В первом случае искомую вероятность можно найти путем интегрирования в пределах от 0 до 0,01l (рис. 12):
 . (1)
. (1)
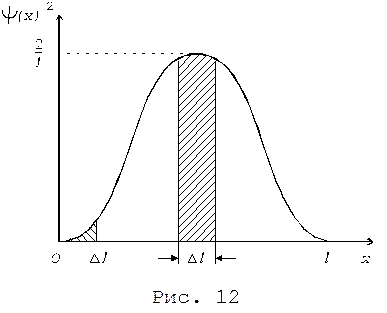
|
Знак модуля в выражении (1) опущен, так как функция 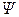 в данном случае не является комплексной. Поскольку x изменяется в интервале 0 £ x £ 0,01l, то px/l << 1 и, следовательно, справедливо приближенное равенство в данном случае не является комплексной. Поскольку x изменяется в интервале 0 £ x £ 0,01l, то px/l << 1 и, следовательно, справедливо приближенное равенство
|
 . (2)
. (2)
С учетом формулы (2) выражение (1) принимает вид
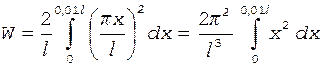 .
.
После интегрирования получаем
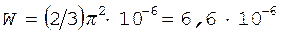 .
.
Во втором случае нет необходимости в интегрировании, так как квадрат модуля волновой функции вблизи ее максимума в заданном малом интервале (Dl = 0,01l) практически не изменяется. Искомая вероятность определяется выражением
 Dl,
Dl,
или
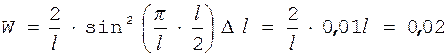 .
.
Пример 4. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить энергию испущенного при этом фотона.
Решение. Энергия фотона определяется по формуле
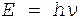 .
.
Здесь неизвестной величиной является частота 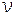 , которая может быть рассчитана по спектральной формуле
, которая может быть рассчитана по спектральной формуле
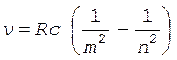 ,
,
где R – постоянная Ридберга (R = 1,1×107 м-1);
с – скорость света в вакууме (с = 3×1 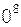 м/с);
м/с);
m – номер орбиты, на которую перешел электрон;
n – номер орбиты, с которой перешел электрон.
Следовательно, энергия фотона выражается форму-лой
E = hRс 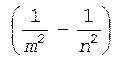 .
.
Подставим в данную формулу значения величин:
 Дж.
Дж.
Пример 5.Вычислить дефект массы и энергию связи ядра 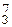 Li.
Li.
Решение. Масса ядра всегда меньше суммы масс свободных протонов и нейтронов. Дефект массы ядра Dm определяется по формуле
Dm = Z×mп+ (A - Z)×mн - mя , (1)
где Z - зарядовое число (атомный номер, или число протонов в ядре);
A - массовое число (число нуклонов, состав-ляющих ядро);
mп, mн, mя - массы протона, нейтрона и ядра соответственно.
В формуле (1) неизвестна масса ядра лития, которая определяется из соотношения
mя = mа - Z×me, (2)
где mа - масса атома;
me - масса электрона.
Подставим соотношение (2) в формулу (1):
Dm = Z×mп + (A - Z)×mн - mа + Z×me. (3)
Массы нуклонов, электрона и атома выразим в атомных единицах массы (а.е.м.), приняв во внимание, что 1 а.е.м.= 1,66×10-27 кг. Тогда после подстановки соответствующих значений в формулу (3) получим
Dm = 3×1,00728+4×1,00867-7,01601+3×0,00065 = 0,04216 а.е.м.
Выразим Dm в килограммах:
Dm = 0,04216×1,66×10-27 = 7×10-29 кг.
Энергия связи определяется по формуле
Есв = Dm×с2 = 7×10-29(3×108)2 = 63×10-13 Дж.
Пример 6. Имеется радиоактивный препарат  Мg массой m = 0,2 мкг. Определить начальную активность препарата Ао и активность препарата А через t = 5 ч. Период полураспада магния
Мg массой m = 0,2 мкг. Определить начальную активность препарата Ао и активность препарата А через t = 5 ч. Период полураспада магния 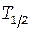 = 10 мин.
= 10 мин.
Решение. Активность изотопа характеризует скорость радиоактивного распада и равна отношению числа ядер dN, распавшихся за интервал времени dt, к этому интервалу:
А = - dN/dt. (1)
Знак "-" показывает, что число радиоактивных ядер N со временем убывает. Для нахождения отношения dN/dt воспользуемся законом радио-активного распада
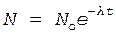 , (2)
, (2)
где N - число радиоактивных ядер, содержащихся в изотопе в момент времени t;
Nо - число радиоактивных ядер в момент времени, принятый за начальный (t = 0);
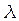 - постоянная радиоактивного распада.
- постоянная радиоактивного распада.
Продифференцируем выражение (2) по времени:
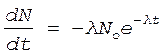 . (3)
. (3)
Из формул (1) и (3) следует, что активность препарата A в момент времени t равна
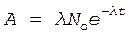 . (4)
. (4)
Если в формулу (4) подставить t = 0, получим на-чальную активность препарата Ао:
Ао=  Nо. (5)
Nо. (5)
Постоянная радиоактивного распада 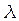 связана с периодом полураспада
связана с периодом полураспада  соотношением
соотношением
 . (6)
. (6)
Число радиоактивных ядер Nо, содержавшихся в изотопе в момент времени, когда его масса была равна m, определяется соотношением
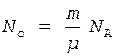 , (7)
, (7)
где 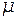 - молярная масса изотопа;
- молярная масса изотопа;
NА - число Авогадро.
С учетом выражения (7) формулы (5) и (4) принимают вид
 ;
;
 . (8)
. (8)
Произведем вычисления, учитывая, что:
1)  = 10 мин = 600 с;
= 10 мин = 600 с;
2)  ;
;
3) t = 6 ч = 6×3,6×103 с = 2,16×104 с.
 Бк;
Бк;
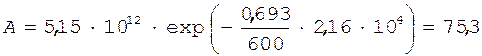 Бк.
Бк.
Дата добавления: 2015-07-24; просмотров: 1604;
