БОРОВСКАЯ ТЕОРИЯ АТОМА ВОДОРОДА

В 1913 году Н.Бор (датский физик), используя представления о квантовом характере излучения и поглощения, предпринял попытку создать качественно новую теорию атома, которая связала бы воедино эмпирические закономерности линейчатых спектров и устойчивость атомов (в рамках планетарной модели атома).

В основу своей теории Бор положил два постулата (утверждения, не имеющих логического обоснования), которые отражали наиболее общие закономерности, экспериментально установленные в атомных спектрах.

Первый постулат: существуют стационарные состояния атома, соответствующие дискретному набору разрешенных значений его энергии W_i. ( i =1,2,3 …). Этим состояниям соответствует набор устойчивых электронных орбит, движение по которым не сопровождается электромагнитным излучением.

Этот постулат Бор дополнил следующим квантовым условием: из всех электронных орбит, возможных по классической теории, допустимы лишь те, для которых величина момента импульса L_e электрона квантована (кратна постоянной Планка), то есть

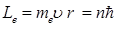. (2.4)

Второй постулат: при переходе электрона из одного стационарного состояния в другое излучается (или поглощается) один фотон с энергией

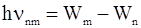, (2.5)

равной разности энергий этих состояний.

При W_n < W_m происходит излучение фотона (переход электрона с более удаленной от ядра орбиты на более близлежащую); при W_n>W_m - поглощение фотона (переход в состояние с большей энергией, т.е. на более удаленную от ядра орбиту).

Набор возможных дискретных частот квантовых переходов

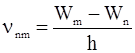(2.6)

и определяет линейчатый спектр атома.

Выдвинутые Бором постулаты, позволили рассчитать спектр атома водорода и водородоподобных атомов (систем, состоящих из ядра с зарядом Z|e| и одного электрона – например, ионов He⁺, Li⁺⁺), а также вычислить теоретически постоянную Ридберга.

Решая совместно уравнение (2.3), предложенное Резерфордом, и уравнение (2.4), получим выражение для радиуса n -ой стационарной орбиты:

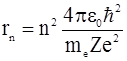, (n=1,2,3...). (2.7)

Для атома водорода (Z =1) радиус первой орбиты электрона (n=1) равен r₁=0,528· 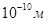, что соответствует расчетам на основе кинетической теории газов.

Полная энергия электрона в водородоподобной системе при допущении неподвижности ядра равна сумме кинетической энергии электрона ( 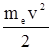) и потенциальной энергии его взаимодействия с ядром ( 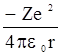). Учитывая соотношения (2.3) и (2.7), получим

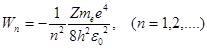, (2.8)

где знак минус означает, что электрон связан в атоме силой притяжения к ядру. Формула (2.8) показывает, что энергия электрона в атоме водорода квантована – она может принимать не любые значения, а лишь определенный набор дискретных значений, определяемый квантовым числом n.

Энергетические состояния атома образуют последовательность энергетических уровней. С ростом n энергетические уровни сближаются. Абсолютное значение W_n в формуле (2.8) считают равным энергии связи электрона в атоме, находящемся в

n-ом состоянии. Энергетическое состояние, соответствующее n=1, называется основным (нормальным) состоянием. Все состояния с n > 1 являются для атома водорода возбужденными. Минимальная энергия атома водорода равна W₁= – 13,55 эВ ( n>1), максимальная W_¥=0 (n = ¥), что соответствует ионизации атома (отрыву от него электрона). Энергия ионизации невозбужденного атома водорода равна

W_i=W_¥ - W₁ =13,55 эВ.

В соответствии со вторым постулатом Бора, при переходе атома водорода (Z =1) из стационарного состояния m в стационарное состояние n с меньшей энергией испускается квант излучения частотой

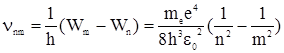
(2.9)

где 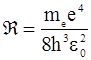- постоянная Ридберга. (2.10)

Значение 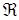, рассчитанное по формуле (2.10), совпадает с ее экспериментальным значением. Это совпадение доказывает правильность полученной Бором формулы (2.8).

Таким образом, теория Бора позволила впервые объяснить наблюдаемые спектры простейших атомов и другие явления, в которых проявляются квантовые закономерности.