Боровская модель атома водорода

Модель этого простейшего атома состоит из положительно заряженного ядра (+е) и одного электрона (-е) (рис 12.5).

Пусть электрон движется со скоростью 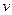по одной из доступных ему траекторий (r_n). Запишем классическое уравнение движения электрона (II закон Ньютона) и квантовое условие Бора.

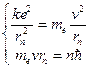(12.2)

Рис. 12.5

Отсюда вытекает условие квантования орбит: электрону в атоме водорода доступны круговые орбиты следующих радиусов:

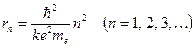(12.3)

Радиус первой орбиты (n = 1) называется боровским радиусом атома r₀. Он составляет

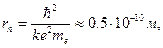
что неплохо согласуется с газокинетическим размером атома.

Вычислим внутреннюю энергию атома, которая складывается из кинетической энергии электрона и потенциальной энергии его взаимодействия с ядром. Запишем при этом и уравнение движения электрона (12.2).

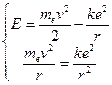
Отсюда следует, что энергия атома

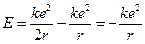(12.4)

Воспользовавшись результатом (12.3) 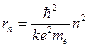, получим спектр энергий, доступных атому:

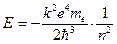(12.5)

При переходе электрона с «n» орбиты на «m»-ю, атом излучает фотон. Его энергия

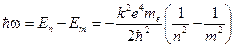(12.6)

Частота этого излучения определяет одну из линий в спектре атома водорода.

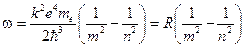(12.7)

Сравнивая этот результат с обобщенной формулой Бальмера, приходим к выводу, что 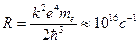— постоянная Ридберга.

Поразительно численное совпадение этой константы, рассчитанное по Бору, с тем значением, которое было получено в результате анализа спектра излучения атома водорода!

Таким образом, уравнение (12.7) дает все частоты, присутствующие в излучении атома водорода. Это был грандиозный успех планетарной модели атома Резерфорда и Боровской теории этой модели.

Теперь понятно, как возникают спектральные линии и серии в атомарном излучении.

На рисунке 12.6 представлен масштабный чертеж пяти низших Боровских орбит водорода.

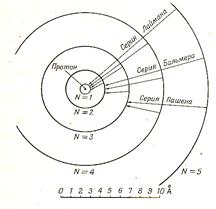
Рис. 12.6

При движении электрона по одной из этих доступных ему орбит, атом находится в стационарном состоянии и не излучает и не поглощает энергию.

При переходе электрона, например, со второй орбиты (N = 2) на первую (N = 1) излучается фотон соответствующей частоты. В спектре излучения этот переход отмечен одной из линий в серии Лаймена.

Эта серия включает частоты фотонов, излучаемых при переходе с любой орбиты на первую.

Все переходы с орбит n > 2 на вторую рождают различные линии серии Бальмера:

.

И так далее.

Боровская теория наглядно объясняет и комбинационный принцип Ритца.

Обратный переход электрона с одной из нижних орбит на более высокую возможен лишь при поглощении атомом энергии извне.

Прямым экспериментальным подтверждением квантованности электронных орбит в атоме и его энергии явился эксперимент Франка и Герца.