Корпускулярно-волновой дуализм излучения

Особенности теплового излучения абсолютно черного тела, фотоэффект, эффект Комптона – неопровержимо свидетельствуют о корпускулярной природе излучения. Излучение – и свет в том числе – поток порций энергии – фотонов. Фотон обладает энергией и импульсом:

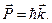
С другой стороны, такие явления как дифракция, интерференция, поляризация убеждают нас в волновой природе излучения. Излучение — электромагнитные волны в широком диапазоне частот.

С третьей стороны, можно вспомнить о давлении, преломлении света, то есть о явлениях, которые можно объяснить как с позиций классической волновой так и квантовой теории света.

Рассмотрим, например, отражение света от плоского зеркала.

Волновая теория связывает давление света Р с объемной плотностью энергии в электромагнитной волне:

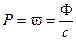
Здесь: 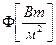— поток излучения.

При отражении света, падающие и отраженные волны образуют стоячую волну, плотность энергии в которой

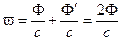
где: Φ — поток отраженного излучения.

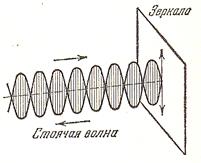
Рис. 11.3

Следовательно, давление излучения на отражающее зеркало

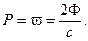
Теперь решим эту задачу считая, что свет – поток фотонов (рис. 11.4).

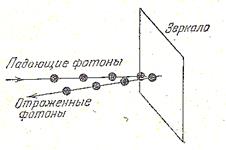
Рис. 11.4

При упругом отражении фотона от зеркала, последнее получает импульс

.

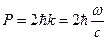При падении в единицу времени N фотонов на единичную поверхность зеркала (1 м²), давление, создаваемое этим потоком частиц, будет равно суммарному импульсу, переданному ими зеркалу.

.

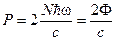Здесь: 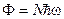— поток энергии падающих фонов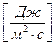

Нетрудно обнаружить, что в рассмотренной задаче классическая волновая и квантовая корпускулярная теории приводят к совпадающим результатам.

Таким образом, мы приходим к выводу, что излучение (свет) в одних случаях проявляет свои волновые свойства, в других – корпускулярные. В этом и состоит «диалектическое единство противоположностей», нашедшее свое отражение в теории корпускулярно-волнового дуализма излучения.

Задача

Фотон рентгеновского излучения с энергией ε = 0.15 МэВ испытал рассеяние на покоившемся свободном электроне, в результате чего его длина волны увеличилась на ∆λ = 0.015 Å. Найти угол φ, под которым вылетел комптоновский электрон отдачи.

Решение:

Рис. 11.5

При упругом столкновении фотона со свободным покоящимся электроном выполняется закон сохранения импульса системы (рис. 11.5)

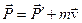
Здесь: 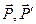— импульсы фотона до и после взаимодействия,

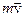— импульс электрона отдачи.

Искомый угол φ легко связать с углом рассеяния фотона θ и с соотношением его импульсов .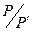

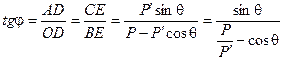(11.7)

Воспользовавшись формулой Комптона, вычислим косинус и синус угла θ:

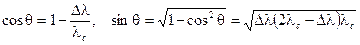
Импульсы падающего и рассеянного фотонов связаны с их энергиями:

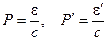
Энергия рассеянного фотона:

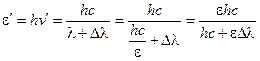
Теперь можно записать новое выражение импульса фотона:

Подставив в исходное уравнение (11.7) известные теперь значения cosθ, sinθ, P и P', после преобразования получим:

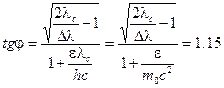
И, следовательно, φ = 49º

Здесь энергия покоя электрона: m₀c² = 0.511 MэВ.

Итог лекции 11.

1. Энергия и импульс фотона:

,

.

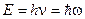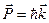Связь импульса фотона с его энергией:

.

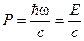2. Энергия и импульс микрочастицы:

.

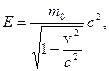
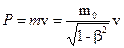Связь энергии и импульса релятивистской частицы:

.

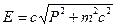3. Эффект Комптона:

.

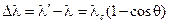Лекция 12 «Боровская теория атома водорода»

План лекции

1. Модель атома Томпсона

2. Спектр атома водорода

3. Опыты по рассеянию α-частиц. Планетарная модель атома Резерфорда

4. Постулаты Бора

5. Опыт Франка и Герца

Итог лекции 12

1. Модель атома Томпсона (1903)

К началу 20-ого века было окончательно установлено, что атом — не неделимая частица вещества. Это сложная конструкция, в состав которой входят и заряженные частицы.

В 1900-м году, изучая природу катодных лучей, английский ученый Джозеф Джон Томпсон (сотрудники его называли «Джи-Джи») измерил удельный заряд электрона. Из этих опытов следовало что электроны обладают массой, которая несомненно много меньше массы самого легкого атома – атома водорода. Было ясно, что электроны являются составными частями всех атомов. Но атомы, как известно, электронейтральны. Это означало, что в атоме наряду с отрицательными электронами присутствуют и положительно заряженные частицы.

Первая электромагнитная не квантовая модель атома была создана Дж. Дж. Томпсоном. В этой работе он руководствовался следующим постулатом Кельвина о силах притяжения между атомом и электроном:

«Притяжение атомом внешнего электрона обратно пропорционально квадрату расстояния между их центрами, а притяжение электрона, находящегося внутри самого атома, пропорционально расстоянию между их центрами».

Такая закономерность характерна для гравитационной силы притяжения тела Землей в предположении, что масса Земли равномерно распределена по объему земного шара. Эта аналогия наводила на мысль о том, что положительный заряд атома равномерно распределен по всему его объему, а электроны атома плавают в этом положительном облаке. В таком случае несложно вычислить силу, действующую на электрон, например, в атоме водорода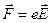

Рис. 12.1.

Для отыскания напряженности поля Е в той точке атома, где находится электрон, воспользуемся теоремой Остроградского-Гаусса (рис. 12.1):

.

Здесь: 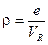— объемная плотность положительного заряда атома.

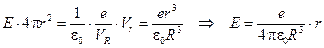
Таким образом, сила, действующая на электрон в подобном атоме, является квазиупругой и непременно приведет к колебаниям электрона относительно центра атома.

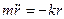
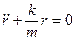
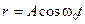
Частота колебаний электрона:

Это выражение позволяет вычислить радиус атома R считая, что атом излучает электромагнитную волну «реальной» частоты ω₀ ≈ 10¹⁵ с^-1.

Такой расчет дает значение радиуса R ≈ 10^-10 м. Этот результат великолепно совпал с известным к тому времени газокинетическим размером атома.

Но это совпадение стало единственным достижением данной модели. Несостоятельность модели Томпсона проявилась в том, что она не могла объяснить известные к тому времени свойства атомов. Например – закономерности атомных спектров.