Эффект Комптона. В истории физики открытие явления Комптона принято считать решающим для победы фотонной теории излучения

В истории физики открытие явления Комптона принято считать решающим для победы фотонной теории излучения. В чем оно заключается?

Известно, что при падении излучения на вещество, часть излучения рассеивается, сохраняя неизменную частоту. Такой характер рассеяния легко объясняется классической волновой теорией излучения.

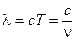Однако в 1923 году молодой американский физик Артур Комптон обнаружил, что при рассеянии рентгеновских лучей, наряду с классическим явлением рассеяния без изменения частоты, можно наблюдать и рассеяние с уменьшением частоты, то есть с увеличением длины волны . Схема эксперимента Комптона приведена на рис. 11.1.

Рис. 11.1.

В опыте Комптона изучалось столкновение фотона с «неподвижным» свободным электроном.

Здесь при рассеянии на угол θ рентгеновских лучей λ обнаруживается излучение с длинной волны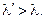

Как свидетельствует эксперимент, разность длин волн рассеянной (λ') и падающей (λ) зависит от угла рассеяния θ:

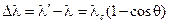. (11.4)

Здесь: λ_с = 0.024Å — размерная постоянная эффекта.

Этот результат – еще один пример явления, необъяснимого с точки зрения волновой теории, но понятного, если его рассматривать с позиции квантовой, фотонной теории излучения.

Эффект Комптона легко объясняется, если предположить, что излучение – поток фотонов. При падении на вещество они упруго взаимодействуют с электронами.

Рассмотрим одно такое взаимодействие: фотон – электрон. Для этого абсолютно упругого удара выполняются законы сохранения энергии и импульса системы .

До «столкновения» импульс системы «фотон – электрон» определяется импульсом фотона .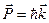

Электрон до столкновения будем считать неподвижным.

Энергия системы фотон – электрон перед ударом складывается из энергии фотона и энергии покоя электрона

.

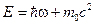После взаимодействия, изменится импульс фотона ( ) и придет в движение электрон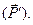

При этом энергия системы будет равна сумме новой энергии фотона и электрона:

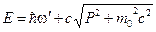
Здесь мы преобразовали энергию микрочастицы –электрона следующим образом:

.

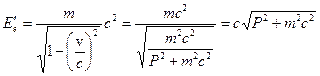Теперь запишем законы сохранения:

энергии:

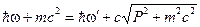и (11.5)

импульса:

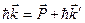. (11.6)

Первое из этих уравнений (11.5) разделим на скорость света:

. (11.7)

Напомним, что волновое число 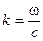. Возведем уравнение (11.7) в квадрат:

.

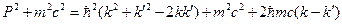Возведем в квадрат и векторное уравнение закона сохранения импульса (11.6):

.

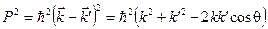Сравнивая два последних выражения, получим:

.

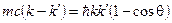Домножим обе части этого уравнения на :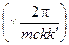

.

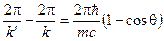Или

.

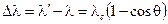Здесь: константа λ_с — комптоновская длина волны электрона.

Теоретический расчет постоянной Комптона дает результат для рассеяния фотонов на свободных электронах 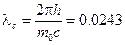Å, великолепно совпадающий с константой, рассчитанной по результатам эксперимента. На рис. 11.2 представлены спектры рассеянного излучения для трех углов рассеяния. Видно, что с увеличением угла рассеяния θ (45⁰, 90⁰, 135⁰) увеличивается разность длин волн (частот) падающего и рассеянного излучения.

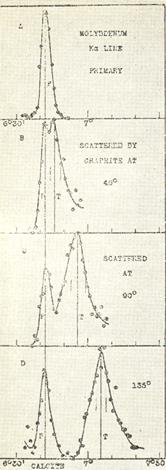
Рис. 11.2
Спектры рассеянного излучения для трех углов рассеяния.

[Из работы Комптона (1923)]