Механика

101.Легковой автомобиль длиной l₁ = 4,5 м, движущийся со скоростью v₁ = 90 км/ч, обгоняет авто-поезд длиной l₂ = 15 м, движущийся со скоростью v₂ = 60 км/ч. Определить длину участка обгона L, т.е. расстояние между точкой, в которой передний бампер автомобиля поравняется с задним бампером автопоезда, и точкой, в которой задний бампер автомобиля поравняется с передним бампером автопоезда. Как изменится L, если скорость автомобиля уменьшится до 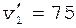км/ч?

102.С помощью рентгеновского лазера, расположенного на круговой орбите H = 150 км, требуется уничтожить крылатую ракету длиной l = 5 м, движущуюся горизонтально со скоростью v = 300 м/с на высоте h = 15 м. Какое расстояние пролетит ракета за промежуток времени между "выстрелом" и ее поражением? Следует ли вводить упреждение в направление лазерного луча?

103. Скорость тела, движущегося прямолинейно, меняется по закону v = A+Bt+Ct², где A = 1 м/с; B = 3 м/с²; C = 6 м/с³. Какое расстояние пройдет тело к моменту времени, когда его ускорение станет равным a = 27 м/с²?

104.Тело движется вдоль оси x согласно уравнению x = A+Bt+Ct²+Dt³, где B = 2 м/с; C = 1 м/с²; D = 0,5 м/с³. Какой путь S оно пройдет за промежуток времени, в течение которого его ускорение возрастет с a₁ = 5 м/с² до a₂ = 11 м/с²?

105. Скорости двух тел, движущихся вдоль оси x, изменяются согласно уравнениям v₁ = A₁+B₁t+C₁t² и v₂ = A₂+B₂t+C₂t², где A₁ = 2 м/с; B₁ = 5 м/с² ; A₂ = 10 м/с; B₂ = 1 м/с² ; C₁ = C₂ = 0,3 м/с³. Первое тело стартует из точки x₁ = 0, а второе - из точки x₂ = 10 м. Определить ускорения тел в момент, когда первое тело догонит второе.

106.Координата колеблющейся материальной точки изменяется по закону x=A·sin(2pnt), где А=4 см, n=2 Гц. Определить скорость и ускорение точки в положении х=1 см.

107.Две точки движутся вдоль оси x согласно уравнениям x₁ = A₁+B₁t+C₁t²+D₁t³ и x₂ = A₂+B₂t+C₂t²+D₂t³, где B₁ = 1 м/с; C₁ = 2 м/с²; D₁ = 0,1 м/с³; B₂ = 2 м/с; C₂ = 0,8 м/с²; D₂ = 0,2 м/с³. Каковы будут скорости точек, когда их ускорения окажутся одинаковыми?

108.Точки движутся вдоль оси x согласно уравнениям x₁ = B₁t+C₁t^-1 и x₂ = B₂t+C₂t², где B₁ = 1 м/с; C₁ = 4 м×с; C₂ = 2 м/с². Определить ускорения точек в момент времени, когда скорость первой из них равна нулю.

109. Две точки движутся вдоль оси x так, что скорость первой из них меняется согласно уравнению v₁ = Bt+Ct², где B = 8 м/с²; C = -1 м/с³, а скорость второй постоянна и равна v₂ = 12 м/с. Определить расстояние между точками, когда их ускорения окажутся одинаковыми, если при t_н = 0 координаты точек были равны x₁ = 0 м и x₂ = 10 м. Каким будет это расстояние через t = 8 с после начала движения?

110.Две точки движутся вдоль оси x согласно уравнениям x₁ = B₁t²+Ct^-1 и x₂ = B₂t, где B₁ = 1 м/с²; C = -8 м×с; B₂ = 2 м/с. Определить скорости точек в момент, когда их ускорения одинаковы.

111.Зависимость пути s, пройденного телом, от времени t определяется уравнением s = At+Bt², где A = -1 м/с; B = 0,5 м/с². В какой момент времени тангенциальное ускорение a_t будет равно нормальному ускорению a_n, если радиус кривизны траектории равен R = 1 м? Определить также полное ускорение a в этот момент времени.

112.Точка 12 движется 12 согласно 12 уравнению s = At+Вt³, где A = 1 м/с; В = 1 м/с³. Определить радиус кривизны траектории в момент, когда полное ускорение равно a = 10 м/с², а нормальное ускорение равно a_n = 8 м/с².

113.Траектория движения точки задается уравнениями x = At и y = Bt², где A = 3 м/с; B = 1 м/с². Определить угол между полным и нормальным ускорениями в момент времени t = 2 с, когда радиус кривизны траектории равен R = 21 м. Начертить траекторию за первые две секунды движения.

114.Траектория движения точки задается уравнениями x = A cos wt и y = B sin wt, где A = B = 1 м; w = 2pс^-1. Начертить траекторию движения и найти ускорение, с которым движется точка.

115.Тело брошено с высоты Н=10 м вверх под углом a=30⁰ к горизонту с начальной скоростью v₀=20 м/c. Записать уравнение траектории тела и определить её кривизну через t=4 c после начала движения.

116.Тело брошено вверх под углом a=60⁰ к горизонту с начальной скоростью v₀=30 м/c. Определить координаты тела, тангенциальное и нормальное ускорения через t=1 c после начала движения.

117.С самолета, летящего со скоростью v=180 км/ч на высоте H=100 м, сбрасывают груз. Определить модуль векторов скорости и перемещения груза до точки падения, а также направление движения груза в момент касания земли.

118.Скорость вращенияколеса радиусом R=1 м изменяется по закону w=w₀-At³, где w₀=32 с^-1, А=4 с^-2. Определить путь, пройденный точками обода колеса до остановки.

119.Угловое перемещение, совершаемое диском радиуса R=0,5 м, изменяется по закону j=Bt-Ct², где B=16 c^-1, C=4 c^-2. Определить ускорение точек обода колеса в момент остановки и число оборотов, которое сделает к этому времени колесо.

120.Колесо вращается равноускоренно и делает N=240 оборотов за время t=2 мин. Определить начальную частоту вращения и угловое ускорение колеса, если в конце движения колесо вращалось с частотой n=600 об/мин.

121. В "рельсотроне", или электромагнитной пушке, снаряд разгоняется магнитным полем. Какова должна быть длина разгонного участка "рельсотрона", чтобы снаряд за t = 0,01 с разгонялся до скорости v = 8 км/с? Считая силу магнитного воздействия на снаряд постоянной, определить, во сколько раз она превышает вес снаряда на поверхности Земли.

122. Скорость шарика, падающего вниз в глицерине, меняется со временем по закону v = v_о(1-e^-at), где v_о = 6,1 см/с; a = 140 с^-1. Определить плотность шарика r_ш, если известно: 1) через t = 0,01 с после начала движения сила вязкого трения по модулю в 3 раза больше равнодействующей всех сил, приложенных к шарику; 2) плотность глицерина равна r_г = 1,25×10³ кг/м³.

123. Сила сопротивления, действующая на пузырек пара, поднимающийся в жидкости, определяется по формуле Стокса F_с = 6pRhv, где R - радиус пузырька; h - коэффициент вязкости жидкости; v - скорость движения пузырька. Определить коэффициент вязкости жидкости, если R = 3 мм, а скорость движения пузырька постоянна и равна v = 0,02 м/с. Плотность пара считать пренебрежимо малой по сравнению с плотностью жидкости r_ж = 1 г/см³.

124. Космонавт массой m = 70 кг проходит испытание во вращающейся центрифуге, сидя в кресле, удаленном от оси вращения на расстояние l = 2 м. Сравните максимальный вес космонавта при вращении центрифуги с частотой n=2 об/с в горизонтальной и вертикальной плоскостях.

125. Проволока выдерживает груз массой m₁=110 кг при вертикальном подъеме его с некоторым ускорением и груз массой m₂ = 690 кг при опускании его с таким же по модулю ускорением. Какова максимальная масса груза, который сможет выдержать эта проволока, если поднимать его с постоянной скоростью?

126. Атлет раскручивает молот (шар массой m = 7 кг, привязанный к тросу) так, что шар движется по окружности радиусом R = 1 м, а путь, пройденный шаром во время раскрутки, растет в соответствии с уравнением s = Bt+Ct², где B = 4 м/с; C = 2 м/с². Трос выдерживает нагрузку F_п = 14 кН. Какой запас прочности имеет трос в момент броска молота, если продолжительность раскрутки t = 4 с?

127. На краю круглой платформы радиусом R = 2,35 м лежит шайба. Платформа вращается так, что путь, проходимый шайбой, растет в соответствии с уравнением s = Ct², где C = 0,5 м/с². В какой момент времени шайба соскользнет с платформы, если коэффициент трения равен m = 0,2?

128. Машина Атвуда, представляющая собой систему из двух тел массами m₁ и m₂ , соединенных невесомой нитью, перекинутой через невесомый блок, может быть использована для взвешивания тел. Определить массу тела m₁ , если тело массой m₂ = 2 кг движется вниз с ускорением a = 1,4 м/с².

129. На краю горизонтальной плоскости установлен невесомый блок, через который перекинута нерастяжимая и невесомая нить, соединяющая два груза, один из которых движется вертикально и имеет массу m₁ = 2 кг, а другой движется горизонтально и имеет массу m₂ = 1,5 кг. Определить ускорение, с которым движутся грузы, если коэффициент трения для плоскости m = 0,2.

130. Молот массой m = 1 т падает на наковальню с высоты H = 127 см. Длительность удара Dt = 0,01 с. Определить среднее значение силы удара.

131. На прямолинейно движущееся со скоростью v=5 м/с тело массой m=2 кг действует в направлении движения убывающая по времени сила F=F₀-At, где F₀=5 Н, А=2,5 Н/c. Каков будет импульс тела по окончании действия силы?

132. Модуль силы, действующей в направлении движения тела, изменяется согласно уравнению F=At-Bt², где А=2 Н/с, B=3 Н/c². Определить изменение импульса тела к моменту окончания действия силы.

133. Тело массой m=2 кг равномерно вращается по окружности радиуса R=20 см. Определить модуль изменения импульса тела при повороте на угол j=60⁰, если период вращения Т=2 с.

134. Определить давление газа на стенки сосуда, если: 1) масса одной молекулы m = 3,3×10^-27 кг; 2) скорость молекулы v = 2 км/с; 3) число молекул, движущихся по нормали к стенке сосуда, составляет n = 10¹⁹ на 1 см³ объема сосуда.

135. Одним из движителей космических кораблей может быть "световой парус" - зеркальная пленка, получающая импульс при падении на нее света. Начальная скорость корабля равна v₁ = 7,9 км/с (первая космическая), конечная скорость равна v₂ = 11,2 км/с (вторая космическая). Сколько фотонов (частиц света) должно отразиться от "светового паруса", если: 1) свет падает на "парус" по нормали; 2) масса корабля с "парусом" m = 500 т; 3) масса фотона m_ф = 0,5×10^-35 кг?

136. Какой импульс получит покоящийся электрон при попадании в него g-кванта, если: 1) масса падающего g-кванта m₁ = 3,3×10^-30 кг; 2) масса рассеянного g-кванта m₂ = 0,71×10^-30 кг; 3) угол между направлениями движения падающего и рассеянного g-квантов равен J = 90°?

137. Фотон падает по нормали на металлическую пластинку и в результате фотоэффекта выбивает из нее электрон, движущийся по нормали в направлении, противоположном направлению движения фотона. Какой импульс получит пластина при попадании в нее одного фотона, если масса фотона m_ф = 5×10^-34 кг, а кинетическая энергия электрона равна T_e = 4,1×10^-19 Дж?

138. Граната, летевшая со скоростью v = 15 м/с, разорвалась на два осколка. Больший осколок, масса которого составляет 60% от массы всей гранаты, стал двигаться под углом a=30^ºк прежнему направлению со скоростью v₁=250 м/с. Найдите модуль скорости v₂ меньшего осколка.

139. Снаряд, летевший в воздухе горизонтально со скоростью v=50 м/с на высоте h=80 м, разорвался на две равные части. Один из осколков полетел вниз и упал на землю через 2 с после разрыва. Определите угол, по отношению к горизонту, в направлении которого полетел второй осколок и его скорость.

140. Для сбора космического "мусора" на околоземной орбите может быть использована сеть-ловушка. С какой скоростью станет двигаться космический "мусорщик" массой m₁ = 50 т, оборудованный такой сетью и имеющий скорость v₁ = 8,050 км/с, после захвата вышедшего из строя спутника массой m₂ = 1 т, двигавшегося в момент захвата в том же направлении, что и "мусорщик", со скоростью v₂ = 8,000 км/с?

141. Тело массой m = 0,5 кг движется прямолинейно так, что его скорость меняется согласно уравнению v = A(1-e^-Dt), где A = 1 м/с; D = 1 с^-1. Определить работу сил, действующих на тело, за первые две секунды движения.

142. Тело массой m = 1 кг, теплоемкость которого C = 453 Дж/К, соскальзывает без начальной скорости с наклонной плоскости высотой h = 1 м. Определить скорость тела в конце плоскости, если, соскользнув, оно нагрелось на DT = 0,015 К.

143. При забивании сваи массой m₁ = 0,5 т копер массой m₂ = 1 т падает с высоты h = 1,5 м. Считая удар копра о сваю неупругим, определить, на какую глубину она погрузится в грунт, если средняя сила сопротивления грунта <F_с> = 200 кН.

144. Пуля массой m пробивает ящик с песком массой 4m и застревает в другом таком же ящике. Начальная скорость пули v = 800 м/c на вылете из 1-го ящика уменьшается в 2 раза. Определить: 1) начальную скорость 1-го ящика с песком; 2) отношение количеств теплоты Q₁/Q₂, выделившихся в 1-м и 2-м ящиках.

145. Тело массой m=5 кг под действием постоянной силы начинает двигаться из состояния покоя равноускоренно и, пройдя путь l=16 м, приобретает скорость v=8 м/с. Найдите максимальную и среднюю мощность N этой силы в процессе движения тела.

146. Потенциальная энергия двух a-частиц, находящихся на расстоянии r друг от друга, вычисляется по формуле U = Lr^-1, где L = 9,56×10^-28 Н×м². До какого минимального расстояния смогут сблизиться a-час-тицы, начинающие двигаться из бесконечности навстречу друг другу с относительной скоростью сближения v = 3×10⁶ м/с?

147. Долбежный станок, мощность двигателя которого равна N = 480 Вт, за t = 5 мин прорезает паз глубиной h = 18 мм и длиной l = 100 мм. Определить КПД привода станка (отношение работы резания к энергии, потребляемой станком), если: 1) увеличение глубины паза за один проход резца, равный l, составляет Dh = 0,5 мм; 2) усилие резания составляет F_р = 1 кН.

148. Пружина сжата на x₁ = 10 см. Какая работа будет совершена при дополнительном сжатии пружины до x₂ = 15 см, если сила упругости в конце сжатия равна F₂ = 150 Н?

149. Определить мощность гидропривода, если при давлении P = 500 кПа поршень, площадь которого S = 100 см², равномерно перемещается на расстояние l = 100 мм за t = 2 с.

150. С двух горок одинаковой высоты H = 9 м одновременно начинают скатываться два шарика массами m₁= 1 кг и m₂ =2 кгнавстречу друг другу. Определить высоту h, на которую поднимутся шарики после абсолютно неупругого столкновения, а также количество теплоты Q, выделившейся при соударении. Трение в системе отсутствует.

151. Рассчитать момент инерции квадратной рамки общей массы 4 кг со сторонами длиной по 0,6 м. Ось вращения проходит через центры 2-х противоположных сторон рамки.

152. Рассчитать момент инерции полого шара массой 6 кг относительно оси, проходящей через его центр. Радиус шара 20 см, радиус полости, расположенной в центре шара, равен 10 см.

153. Обруч диаметром D =1 м и массой m =400 г раскручивается вокруг оси, проходящей через его центр и перпендикулярной к его плоскости. Уравнение движения обруча имеет вид: j=А+Bt+Сt², где С=0,5 с^-2. Определить крутящий момент, действующий на обруч.

154. На краях доски длиной L=3 м и массой M=30 кг сидят дети массой по m₁=20 кг каждый. Доска уравновешена на опоре, проходящей через её центр. С каким угловым ускорением начнет двигаться доска, если один из детей создаст вертикальное усилие F=15 Н.

155.К невесомой нити, намотанной на однородный цилиндрический барабан массой m₁ = 2 кг, привязан груз массой m₂ = 4 кг. Ось вращения барабана горизонтальна и неподвижна. С какой скоростью будет двигаться груз через t = 2 с после того, как его отпустили?

156. Два груза, массы которых равны m₁ = 1,5 кг и m₂ = 0,5 кг, соединены невесомой нитью, перекинутой через блок, который представляет собой пустотелый шкив массой m₃ = 1 кг. Тяжелый груз висит на 0,5 м выше более легкого груза. Определить время, через которое грузы окажутся на одной высоте.

157. На краю горизонтальной плоскости установлен блок, представляющий собой однородный диск диаметром d = 6,6 см. Масса блока равна m = 3 кг. Через блок перекинута нерастяжимая невесомая нить, соединяющая два груза, один из которых движется вертикально и имеет массу m₁ = 2 кг, а другой движется горизонтально и имеет массу m₂ = 1,5 кг. Коэффициент трения для плоскости равен m = 0,1. Сколько оборотов N сделает блок за промежуток времени Dt = 0,5 с после начала движения?

158. На однородный барабан массой m = 3 кг действует тормозящий момент M = 15 мН×м так, что угловая скорость w барабана меняется со временем согласно уравнению w = B+Ct, где B = 16 с^-1; С = -1 с^-2. Определить: 1) диаметр барабана; 2) число оборотов, которое он сделает до полной остановки.

159. Стержень длиной L=1 м закреплен в точке, отстоящей от его верхнего конца на 20 см. Стержень отклонили от вертикали на угол 30^º и отпустили. Определить угловое e и тангенциальное a_t ускорение нижнего конца стержня в начальный момент движения.

160. Определить момент сил M, действующих на пулю калибра d = 7,62 мм и массой m = 10 г в стволе винтовки длиной l = 0,6 м, если известно: 1) пуля представляет собой однородный цилиндр; 2) при вылете из ствола пуля успевает сделать N = 4 полных

оборота и имеет скорость v = 600 м/с; 4) пуля в стволе движется равноускоренно.

161. Определить высоту, на которую может подняться шар, запущенный со скоростью v₀=4 м/c вверх по наклонной плоскости. Трением пренебречь. Шар вращается без проскальзывания.

162. Определить линейную скорость вершины спиленного дерева в конце падения. Дерево считать однородным стержнем длиной l = 15 м.

163. Стержень длиной 1,5 м может вращаться относительно оси, отстоящей на 0,5 м от одного из его концов. Стержень поставили вертикально более длинной частью вверх и отпустили. Определить его угловую скорость и линейные скорости концов стержня в момент прохождения им нижнего вертикального положения.

164. При отказе двигателя вертолета и остановке винта, произошедшей на высоте h₁ = 600 м, пилот перешел в режим авторотации и винт стал раскручиваться потоком воздуха, набегающим при падении вертолета.

Определить высоту h₂, на которой возможно возникновение подъемной силы винта, если известно:

1) подъемная сила возникает при скорости вращения винта n = 900 об/мин;

2) винт имеет четыре лопасти, каждую из которых можно считать однородным стержнем длиной l = 4 м и массой m_л = 50 кг;

3) масса вертолета (без винта) m_в = 1 т;

4) скорость падения вертолета на высоте h₂ равна v = 20 м/с.

165. Вагонетка массой m₂ = 0,5 т перемещается за счет энергии гироаккумулятора, представляющего собой вращающийся вокруг своей оси однородный цилиндр массой m₁ = 100 кг и диаметром d = 0,5 м. Определить коэффициент сопротивления при движении вагонетки (отношение силы сопротивления к суммарному весу вагонетки и гироаккумулятора), если при начальной частоте вращения гироаккумулятора n = 70 об/с максимальное расстояние, которое может пройти вагонетка, составляет s = 0,5 км.

165. Манипулятор за t = 2 с равноускоренно перемещает груз массой m = 5 кг по дуге, радиус которой равен R = 1,5 м. Определить максимальную мощность привода манипулятора, если известно: 1) момент

инерции манипулятора J = 15 кг×м²; 2) угол поворота Dj = 90°; 3) груз можно считать точечной массой.

166. На вращающееся тело действует механический момент, изменяющийся по закону М=М₀+At, где М₀=100 Н×м, А=200 (Н·м/c). На сколько изменится момент импульса этого тела за время t=1,5 с?

167. Горизонтальная платформа массой 100 кг и радиусом 1 м вращается с частотой n₁=0,5 об/c вокруг вертикальной оси, проходящей через центр инерции платформы. Человек массой 60 кг стоит на краю платформы. С какой частотой n₂ будет вращаться платформа, если человек сойдет с платформы? Считать платформу диском, а человека материальной точкой.

168. Фигурист массой m=70 кг начинает вращение с частотой n₁=1 об/c, держа руки горизонтально. С какой частотой он будет вращаться, если поднимет руки вертикально? Тело фигуриста считать однородным цилиндром радиуса 15 см, руки – стержнями по 0,75 м и массой по 5 кг каждый.

169. Во вращающийся с угловой скоростью w₁=5 с^-1 диск массой M=10 кг и радиусом R=10 см попадает пуля массой m=10 г со скоростью v=600 м/с. Определить угловую скорость вращения диска с пулей w₁ и работу, совершенную силами сопротивления, если направление полета пули лежало в плоскости вращения диска на расстоянии 5 см от его оси вращения.

170. На вращающийся диск массой М=2 кг и радиуса R₁=1 м бросают без вращения обруч массой m=1 кг радиуса R₂=0,5 м. На сколько изменится угловая скорость вращения системы, если после падения обруча на диск его центр будет находиться на расстоянии l=0,25 м от оси вращения диска? Начальная скорость вращения диска w₁= 2 c^-1.