АТТЫ ДЕНЕЛЕР МЕХАНИКАСЫ
Нақты денелер түсірілген күштердің әсерінен аздап болса да деформацияланады және олардың кейбір бөліктері бір-бірімен салыстырғанда орын ауыстыруы да мүмкін. Олай болса, қатты денелердің қозғалысын қарастырғанда абсолют қатты дене ұғымын енгізіп, оны түсірілген күштер әсерінен мүлде деформацияланбайтын жорамал дене деп ұғу керек.Абсолют қатты денедеп, қандай жағдай болмасын деформацияға ұшырамайтын және барлық жағдайда да осы дененің екі нүктесінің ара қашықтығы (немесе дәлірек айтқанда екі бөлшектің ара қашықтығы) тұрақты болып қалатын денені айтады. Абсолют қатты дененің жеке бөліктерінің бір-бірімен салыстырғанда орын ауыстыруы мүмкін емес. Қатты дененің жазықтықтағы қозғалысын екі қарапайым ілгерілемелі және айналмалы қозғалыстың қосындысы деп қарастыруға болады.
Қатты денеде ойша жүргізілген түзудің өзіне-өзі параллель орын ауыстыруын ілгерілемелі қозғалыс деп түсіну керек. Ол түзу сызықты, қисық сызықты болуы мүмкін. Қозғалыстың бұл түрінде дененің барлық нүктелері ұқсас траектория сызады.
Айналмалы қозғалыс дегеніміз қозғалыс кезінде дененің барлық нүкте-лері шеңберлер сызатын және ол шеңберлердің центрлері айналыс осі деп аталатын бір түзудің бойында жататын қозғалыс.
Жалпы алғанда дене бір мезгілде әрі ілгерілемелі, әрі айналмалы қозғалыста бола алады. Айналмалы қозғалысты сипаттайтын кинематика-дағы бұрыштық шамаларға (бұрыштық жол, бұрыштық жылдамдық, бұрыштық үдеу) толық тоқталып өткен болатынбыз.
Қатты дененің айналысын оқып үйренгенде инерция моменті деген түсінікті қолданамыз.
Жүйенің оське қатысты инерция моменті деп нүктелер массаларының олардың осьтен ара қашықтығының квадратына көбейтінділерінің қосындысына тең шаманы айтады: n
I=S mi ri 2 (5.1)
i=1
Ал материалдық нүкте үшін: I=m r 2 (5.2)
Егер дене біртекті болса, онда оның инерция моменті мынаған тең:
I=ò R2dm=r ò R2dV (5.3)
мұндағы dm-элементар dV көлемнің массасы, r-тығыздық. Интеграл дененің толық көлемі бойынша алынады.
Осыдан көретініміздей, дененің инерция моменті оның массасынан, берілген оське қатысты массаның таралуынан (бөлінуінен) тәуелді, яғни инерция моменті ілгерілемелі қозғалыстағы массасның атқаратын ролі сияқты айналмалы қозғалысқа қатысты дененің инерттілік өлшемі болып табылады.
Ұзындығы l стерженьге перпендикуляр және оның қақ ортасы арқылы өтетін оське қатысты инерция моменті: I=ml2/12 (5.4)
Радиусы R тұтас цилиндрдің оның осіне қатысты инерция моменті:
I =mR2/2 (5.5)
Радиусы R жұқа дененің диаметрі арқылы өтетін оське қатысты инерция моменті: I =mR2/4 (5.6)
Радиусы R шардың оның центрі арқылы өтетін оське қатысты инерция моменті: I = 2mR2/5 (5.7)
Кез келген оське қатысты инерция моменті I берілген оське параллель және дененің массалар центрі арқылы өтетін оське қатысты Ic инерция моменті мен дененің массасының осьтер арасындағы ара қашықтығының квадратына көбейтіндісінің қосындысына тең: I=Ic+md2 (5.8)
(5.8) өрнек Штейнер теоремасы деп аталады.
Қозғалмайтын айналу осі бар қатты дененің кинетикалық энергиясы оның жеке бөліктерінің кинетикалық энергияларынан құралады:
n n
Ek = S Eki = w 2 /2 S mi Ri 2 =I w 2 /2 (5.9)
i=1 i=1
Сонда айналмалы қозғалыстағы дененің кинетикалық энергиясы келесі өрнекпен жазылады Ek=Iw2/2 (5.10)
Дененің жазық қозғалысы жағдайында, мысалы, көлбеу жазықтық бойымен сырғанамай, домалап келе жатқан цилиндрдің қозғалыс энергиясы ілгерілемелі және айналмалы қозғалыстардың энергияларының қосынды-сынан тұрады: E=mvс2/2+Iс w 2/2 (5.11)
мұндағы m–сырғанап бара жатқан дененің массасы, vс-дененің массалық центрінің жылдамдығы, Iс–дененің массалық центрі арқылы өтетін оське қатысты инерция моменті, w-дененің бұрыштық жылдамдығы;
 М
М
b B
R F
О
a
l A
10 – сурет 11- сурет
Айналмалы қозғалыс кезінде массаның ролін инерция моменті, ал сызықтық жылдамдықтың ролін бұрыштық жылдамдық атқаратынын білеміз, ендеше F күштің осьтің кейбір 0 нүктесіне қатысты күш моменті М деп келесі өрнекпен анықталатын векторлық шаманы айтады:M=[rF](5.12)
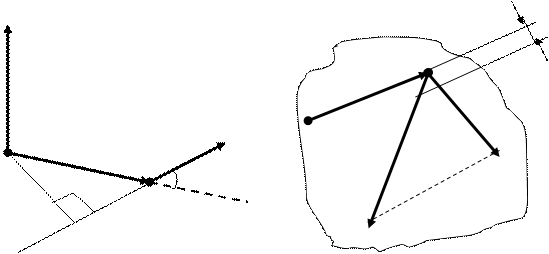
Мұндағы r-радиус вектор, ал l-күш иіні деп аталады. М векторының бағыты бұрғы ережесі бойынша анықталады. Күш моменті денені берілген осьтен айналдыра алу қабілетін сипаттайды. Қозғалмайтын О нүктесіне қатысты күш моменті дегеніміз О нүктесінен күш түсіп тұрған А нүктесіне дейін жүргізілген радиус-вектор мен күштің векторлық көбейтіндісі арқылы анықталатын физикалық шама (10-сурет), мұндағы М–псевдовектор, оның бағыты бұранданы r векторынан Ғвекторына қарай айналдырғандағы оң бұранданың ілгерілемелі қозғалысына сәйкес келеді. Күш моментінің модулі M=Frsina=Ғl (5.13)
мұндағы a-rменFвекторлары арасындағы бұрыш. rsina l –күш иіні, күш әсер ететін сызық пен О нүктесі арасындағы ең қысқа аралық.
Қатты дененің айналысы кезіндегі сыртқы күштердің жұмысын анықтайық (11-сурет). Айналу осінен r қашықтықта орналасқан В нүктесіне Ғ күш түсірілген. Күштің бағыты мен rрадиус-вектордың арасындағы бұрыш-a. Қарастырып отырған дене абсолют қатты дене болғандықтын осы күштің жұмысы денені түгелімен бұруға кеткен жұмысқа тең. Денені өте аз dj бұрышқа бұрғандағы күш түсу нүктесі ВdS=rdj жол жүреді және жұмыс күштің ығысу бағытына проекциясы мен ығысу шамасының көбейтіндісіне тең: dA=Ғsina rdj (5.14)
(5.13) ескере отырып, келесі өрнекті жазамыз dA=Mz dj (5.15)
мұндағы Frsina=Ғl=Mz – z осіне қатысты күш моменті. Соныменен, дененің айналуы кезіндегі жұмыс әсер етуші күш моменті мен бұрылу бұрышының көбейтіндісіне тең.
Денені айналдыру кезіндегі жұмыс оның кинетикалық энергиясының артуына жұмсалады: dA =dT, бірақ dT = d(Jzw2/2) = Jzw dw сондықтан Mz dj = Jzw dw немесе Mz ( dj/dt) =Jzw(dw/dt) w=dj/dt екенін ескерсек, келесі өрнек шығады Mz=Jz(dw/dt)=Jze (5.16)
(5.16) теңдеу қозғалмайтын оське қатысты қатты дененің айналмалы қозғалысының динамика теңдеуі болып табылады. Айналмалы қозғалысты ілгерілемелі қозғалыспен салыстырғанда әрқашанда олардың арасындағы сәйкестікті қарастырады. Сондай сәйкестіктердің бірі ілгерілемелі қозға-лыстағы импульс шамасына айналмалы қозғалыста импульс моменті болып табылады. Қозғалмайтын нүктеге қатысты материалдық нүктенің импульс моменті дегеніміз келесі векторлық көбейтінді арқылы анықталатын физикалық шама болып табылады: L=[rp]=[rmv] (5.17)
мұндағы r-қозғалмайтын нүктеден материалдық нүктеге дейін жүргізілген радиус-вектор; mv–материалдық нүктенің импульсі; L–псевдовектор, оның бағыты оң бұранданы rвекторынан p векторына қарай бұраған кездегі оның ілгерілемелі қозғалысының бағытына сәйкес келеді.
Импульс моменті векторының модулі L=rpsina=mvrsina=pl (5.18)
мұндағы a-rжәне p векторларының арасындағы бұрыш, l-қозғалмайтыннүктеге қатысты p векторларының иіні.
Оське қатысты қатты дененің импульс моменті жекелеген бөлшектерінің импульс моменттерінің қосындысына тең:
n n n
Lz=S mivi ri =S mi r2i w=wS mi ri2=Jzwяғни Lz=Jzw(5.19)
i=1 i=1 i=1
Осытеңдеудіуақыт бойынша дифференциялдасақ, онда:
dLz/dt=Jzdw/dt=Jze=Mz яғни dLz/dt=Mz
Бұл өрнек те қозғалмайтын оське қатысты қатты дененің айналмалы қозғалысының динамика теңдеуі болып табылады: оське қатысты қатты дененің импульс моментінің туындысы осы оське қатысты күш моментіне тең. Вектор түрінде жазатын болсақ dL/dt=M(5.20)
Тұйық жүйеде сыртқы күштердің моменті M=0 және dL/dt=0, осыдан
L= const (5.21)
(5.20) өрнек импульс моментінің сақталу заңы болады: тұйық жүйеде импульс моменті сақталады, яғни уақыт өтуіне қарай өзгермейді.
Импульс моментінің сақталу заңы-табиғаттың фундаментальды заңы болып табылады. Ол кеңістіктің симметриялылығы-изотроптығымен байланысты. Айналмалы қозғалыс динамикасының теңдеуі қатты денелердің қозғалысы денеге әсер ететін күштер және осы күштердің
моменттері арқылы анықталады.
Қатты дене тепе-теңдік күйде болуы үшін мына шарттардың орындалуы қажет:
1. Денеге түсірілген барлық сыртқы күштердің векторлық қосындысы
нольге тең болуы тиіс.
2. Кез келген қозғалмайтын оське қатысты сыртқы күштердің моменті
нольге тең болуы тиіс.
Дененің айналмалы қозғалысын сипаттайтын шамалар мен қозғалмайтын оське қатысты айналысын анықтайтын теңдеулерін және оның ілгерілемелі қозғаласының сипаттамаларын салыстыру 1-кестеде көрсетілген.
1-кесте.
| Ілгерілемелі қозғалыс | Айналмалы қозғалыс | ||
| Физикалық шама | Белгіленуі немесе формуласы | Физикалық шама | Белгіленуі немесе формуласы |
| Масса Жылдамдық Үдеу Күш Импульс Динамиканың негізгі теңдеуі Жұмыс Кинетикалық энергия | m v=dr/dt a=dv/dt F p=m v F=ma F=dp/dt dA =Fs dS mv2/2 | Инерция моменті Бұрыштық жылдамдық Бұрыштық үдеу Күш моменті Импульс моменті Динамиканың негізгі теңдеуі Жұмыс Кинетикалық энергия | I w=dj/dt e=dw/dt Mz немесе М Lz=Jzw Mz=Jze M = dL /dt Mz dj Jzw2/2 |
Дата добавления: 2015-08-08; просмотров: 3510;
