СОҚҚЫ

1. Соққы.Импульс пен энергияның сақталу заңдарынан физиканың есептерін шешуге мысалдар ретінде абсолют серпімді және серпімсіз денелердің соққысы қарастырылады.

Соққы (немесе соқтығысу) дегеніміз екі немесе бірнеше дененің аз уақыт аралығында әсерлесуі.

«Соққы» деген ұғымды қозғалыстағы қатты денелердің әсерлесуі, немесе қатты денелердің сұйықтармен және газдармен кейбір өзара әсерлесуі кезіндегі құбылыстар (гидравликалық соққы, жарылыс және т.б.) арқылы түсіндіруге болады.

Қатты денелердің соқтығысуы кезінде олардың деформациялануы болады. Соқтығысудан кейін дененің пішіні (формасы) қайтадан қалпына келетін болса, соққы серпімді деп аталады.

Денелердің жанасу нүктелері арқылы өтетін олардың жанасу жазықтығына нормаль соққы сызығы деп аталады. Егер денелер соқтығысқанға дейін олардың центрлері арқылы өтетін түзудің бойымен қозғалатын болса, онда соқтығысу орталық (центрлік) соққы деп аталады.

2. Абсолют серпімді соққы. Денелердің механикалық энергиясы энергияның басқа түріне айналмаған соқтығысуды абсолют серпімді соқтығысу деп атайды. Мұндай соқтығысу кезінде кинетикалық энергия серпімді деформацияның потенциалдық энергиясына айналады. Соқтығысқаннан кейін денелер бірін-бірі тебеді де бастапқы пішініне қайта оралады. Нәтижесінде серпімді деформацияның потенциалдық энергиясы қайтадан кинетикалық энергияға өтеді.

Абсолют серпімді соқтығысуда импульстің және механикалық энергияның сақталу заңдары орындалады.

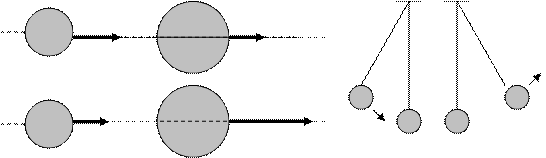
Массалары m₁ және m₂ шарлардың соқтығысқанға дейінгі жылдамдықтарын v₁ және v₂, ал соқтығысқаннан кейінгі жылдамдықтарын v^'₁ және v^'₂ деп белгілейік (8-сурет). Түзу орталық соққы кезінде шарлардың жылдамдық векторлары соққыға дейін және кейін олардың центрлерін қосатын түзудің бойында жатады. Олардың бағыттарын таңбаларымен ескереміз: оң таңбаңы оңға қарай бағыттаймыз, теріс таңбаны солға қарай бағыттаймыз.

m₁ m₂

v₁ v₂

m₁ m₂

v^' ₁ v^' ₂

8-сурет 9-сурет

Осы бойынша сақталу заңдары келесі түрде жазылады

m₁ v₁ + m₂ v₂ = m₁ v' ₁ + m₂ v' ₂ (4.1)

(m₁v²₁)/2+(m₂v²₂)/2=(m₁v₁'²)/2+(m₂v₂'²) ­­­ (4.2)

(4.1) және (4.2) өрнектерін түрлендіруден кейін келесі өрнектерді аламыз:

m₁(v₁-v'₁)=m₂(v₂' -v₂) (4.3) m₁(v²₁-v'²₁)=m₂(v₂'²–v²₂) (4.4)

осыдан v₁+v'₁=v₂'+v₂ (4.5)

(4.3) және (4.5) теңдіктерді шеше отырып, келесі шамаларды табамыз

v'₁=( (m₁– m₂) v₁+2 m₂ v₂)/ (m₁+m₂) (4.6)

v'₂ =((m₂–m₁)v₂+2 m₁v₁)/ (m₁+m₂) (4.7)

Мысалдар келтірейік.

1) v₂=0 болсын v'₁=((m₁–m₂)v₁)/(m₁+m₂) (4.8) v'₂=2m₁v₁/(m₁+m₂) (4.9)

а) m₁ = m₂ . Егер екінші шар соққыға дейін тыныштықта ілініп тұрған болса (v₂=0) (9-сурет), онда соққыдан кейін бірінші шар тоқтайды (v'₁= 0), ал екінші шар бірінші шар соққыға дейін қандай жылдамдықпен қозғалса сол жылдамдықпен сол бағытта қозғалады (v'₂=v₁);

б) m₁>m₂. Бірінші шар соққыға дейінгі бағытында қозғалысын жалғастыра береді, бірақ жылдамдығы азаяды (v'₁<v₁). Соққыдан кейін екінші шардың жылдамдығы бірінші шардың соққыдан кейінгі жылдамдығынан үлкен болады (v'₂ >v'₁) (10-сурет).

в) m₁<m₂. Соққы кезінде бірінші шардың бағыты өзгереді-шар кері бағытта кетеді. Ал екінші шардың бағыты соққыға дейінгі бірінші шардың бағытындай болады, бірақ жылдамдығы аз болады, яғни v'₂< v₁ (11-сурет).

г) m₂>>m₁. (мысалы, шардың қабырғамен соқтығысы). (4.8) және (4.9) теңдеулерінен шығатыны v'₂ = - v₁, » 2 m₁v₁/ m₂ »0.

2) m₁ = m₂ болғанда (4.6) және (4.7) өрнектері келесі түрде жазылады

v'₁= v₂, v'₂= v₁ ,

яғни массалары бірдей болатын шаралар жылдамдықтарымен «алмасады».

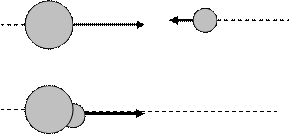
3. Абсолют серпімсіз соққы. Абсолют серпімсіз соққы-соққы нәтижесінде екі дене тұтас дене сияқты бірге қозғалады. Абсолют серпімсіз соққыны көрсету үшін бір-біріне қарама-қарсы келе жатқан екі шардың қозғалысын қарастырамыз (12-сурет).

m₁ v₁ m₂ v₂=0 m₁ v₁ m₂ v₂=0

m₁ v^,₁ m₂ v^,₂

v^,₁ m₁ m₂ v^,₂

10-сурет 11-сурет

Егер шарлардың m₁ және m₂, ал соқтығысқанға дейінгі жылдамдықтары v₁ және v₂ болса, онда импульстің сақталу заңын қолданып, келесі өрнекті жазуға болады m₁ v₁+m₂v₂ =(m₁+m₂)v (4.10)

осыдан v=(m₁v₁ + m₂ v₂)/ (m₁+m₂) (4.11)

Егер шарлар бір-біріне қарама-қарсы қозғалып келе жатқан болса, онда олар импульсі үлкен шардың бағытымен қозғалысын жалғастырады. Жекелеген жағдайда егер шарлардың массалары бірдей болса (m₁=m₂), онда v=(v₁+v₂)/2

m₁ v₂ m₂

v₁

m₁₊ m₂

v

12-сурет.

Орталық абсолют серпімсіз соққы кезінде шарлардың кинетикалық энергиялары қалай өзгеретіндігін анықтайық. Шарлар өзара соқтығысқан кезде олардың арасында деформацияның өзінен тәуелді болмайтын, ал олардың жылдамдықтарынан тәуелді болатын күштер әсер етеді, сонда біз үйкеліс күші сияқты күшті кездестіреміз, сондықтан да механикалық энергияның сақталу заңы орындалмайды. Деформация әсерінен кинетикалық энергияның «жоғалады» да жылу немесе энергияның басқа формасына өтеді. Осы «жоғалуды» денелердің соққыға дейінгі және кейінгі кинетикалық энергияларының айырмасы арқылы анықтауға болады:

DW= ((m₁v²₁)/2 + (m₂v²₂)/2) –( (m₁+m₂)v²)/2

(4.11) формуланы қолдана отырып, келесі өрнекті аламыз

DW=(m₁ m₂ (v₁–v₂)²)/ 2 (m₁ + m₂) сонда

v= m₁v_1/(m₁+m₂), DW= (m₂m₁v²₁)/2(m₁+m₂)

m₂>>m₁ болғанда (тыныштықтағы дененің массасы өте үлкен), v<<v₁ және соққы кезінде барлық кинетикалық энергиясы энергияның басқа түріне өтеді.

Соқтығысқан кезде денелердің кинетикалық энергиясы толығынан немесе жартылай ішкі энергияға айналса, соқтығысқаннан кейін денелер не бірдей жылдамдықпен қозғалатын болса немесе тыныштықта болса, соқтығысу абсолют серпімсіз болады.