ЖҰМЫС ЖӘНЕ ЭНЕРГИЯ

1. Жұмыс. Энергия.Материяның әртүрлі пішіндегі қозғалыстарымен оларға қатысты өзара әсерлесудің сандық өлшемдері болатын физикалық шама энергия деп аталады. Энергияның халықаралық бірліктер жүйесіндегі өлшем бірлігі-джоуль. Қозғалыс материяның бөліп қарастыруға болмайтын қасиеті. Сондықтан да кез келген дененің, жүйенің немесе кез келген өрістің энергиясы болады. Материя қозғалысының түріне байланысты энергияның да әр түрі болады: механикалық, жылулық, электромагниттік, ядролық және т.б. Кейбір құбылыстарда материя қозғалысының түрі (пішіні) өзгермейді (мысалы, ыстық дене суық денені ысытады), басқаларында–қозғалыстың басқа түріне өзгереді (мысалы, үйкеліс кезінде механикалық қозғалыс жылулық қозғалысқа айналады). Бірақ та барлық жағдайда бір денеден екіншісіне берілген энергия осы екінші дененің алған энергиясына тең болады.

Дененің механикалық қозғалысының өзгеруі басқа денелер тарапынан әсер еткен күштерден болады. Өзара әсерлесуші денелер арасындағы энергия алмасудың сандық сипаттамасы механикада күштің жұмысы деген шама арқылы түсіндіріледі.

Түзу сызықты қозғалыстағы денеге орын ауыстыруға a бұрыш жасай F күш әсер ететін болса, онда осы F әсер ететін күштің атқаратын жұмысы күштің орын ауыстыру бағытына проекцисының F_S күш түскен нүктесінің орын ауыстыруының көбейтіндісіне тең:

A=F_S S=FS cos a (3.1)

Жалпы жағдайда күштің модулі де бағыты да өзгеруі мүмкін, сондықтан да бұл жағдайда (3.1) формуланы қолдануға болмайды. Егер орын ауыстырудың dr аз ғана бөлігін қарастыратын болсақ, онда әсер ететін F күшті тұрақты деп қарастыруға болады.

F_S

dA

F 1

F_S v 2

A

dr

1

S

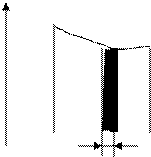
6 – сурет dS

7–сурет

Дененің dr орын ауыстру кезінде F күштің жасаған жұмысы элементар жұмыс деп аталатын скаляр шамаға тең: dA=Fdr=Fcosa dS=F_Sds мұндағы a-Fжәне drвекторлары арасындағы бұрыш. dS=½dr½-элементар жол, F_S–F векторының dr–векторына проекциясы. Траекторияның 1-нүктесінен 2-нүктесіне дейінгі жол бөлігіндегі жұмыс осы траектория бөліктеріндегі элементар жұмыстардың алгебралық қосындысына тең. Бұл қосынды интеграл түрінде беріледі:

_{2 2}

A=ò FdScosa=ò F_S dS (3.2)

^{1 1}

Егер осы тәуелділік график түрінде берілсе, онда жұмыстың мәні 7-суреттегі боялған фигура ауданы бойынша анықталады. Егер a<p/2 болса, күштің атқарған жұмысы оң болады, бұл жағдайда F күштің бағыты қозғалыс жылдамдығының бағытымен бағыттас болады (6-сурет). Егер a>p/2 болса, күштің атқарған жұмысы теріс болады. a=p/2 болса (күш орын ауыстыруға перпендикуляр бағытталған), күштің атқарған жұмысы нольге тең болады. Жұмыстың өлшем бірлігі-джоуль.

2. Қуат. Механикалық энергия түрлері.Жұмыстың жасалу жылдамды-ғын сипаттау үшін қуат деген физикалық ұғым енгізіледі. N=dA/dt (3.3)

dt уақыт ішінде F күш Fdr жұмыс жасайды және қуат мына шамаға тең болады: N=(Fdr/dt)= Fv(3.4)

Қуаттың халықаралық бірліктер жүйесіндегі өлшем бірлігі-ватт.

Жүйенің механикалық қозғалыс энергиясы кинетикалық энергия деп аталады. Тыныштықта тұрған денеге әсер ететін F күш ол денені қозғалысқа келтіреді де жұмыс жасайды, ал қозғалысқа келген дененің энергиясы істелген жұмыс шамасына тең шамаға артады. Соныменен, дене жылдамдығын 0-ден v-ға дейін арттыруға кеткен уақытта жүріп өткен жолында Fкүштің жасаған жұмысы дененің кинетикалық энергиясының артуына кетеді, яғни dA=dT

Ньютонның екінші заңын қолданып F=m(dv/dt), теңдіктің екі жағын да drорын ауыстыруғакөбейтсек келесі теңдік шығады: Fdr=m(dv/dt)dr=dA.

v=dr/dt ескерсек, онда dA=mvdv=mvdv=dT осыдан

_v

T=ò mvdv=mv²/2 (3.5)

⁰

Соныменен, v жылдамдықпен қозғалған массасы m дененің кинетиткалық энергиясы T=mv ²/2 болады. (3.5) формуладан көретініміздей, кинетикалық энергия дененің массасы мен жылдамдығынан тәуелді болады, яғни жүйенің кинетикалық энергиясы оның қозғалыс күйінің функциясы болады.

Потенциалдық энергия-жүйені құрайтын денелердің өзара орналасуымен анықталатын және олардың арасындағы өзара әсерлесу күшімен сипатталатын механикалық энергияның түрі. Денелердің өзара әсері күш өрістері арқылы жүзеге асады. Осындай өрістегі олардың бір орыннан екінші бір орынға орын ауыстырған кезде әсер еткен күштің жұмысы дене қандай траекториямен қозғалатынына тәуелді болмай, тек оның бастапқы орны мен соңғы орнына тәуелді болады. Мұндай өрістер потенциалды деп аталады, ал оларға әсер ететін күштер консервативті күштер деп аталады. Мысалы, серпімді, гравитациялық күштер. Егер дене бір орыннан екінші бір орынға орын ауыстырған кезде оған әсер еткен күштің жұмысы дене траекториясына тәуелді болса, ондай күштер диссипативті (консервативті емес) күштер деп аталады. Оған мысал үйкеліс күші.

Дене потенциалды өрісте орналасқанда оның потенциалдық энергиясы болады. Консервативті күштердің жұмысы потенциалдық энергияның кемуі есебінен істелетіндіктен, оның мәні потенциалдық энергияның теріс таңбамен алынған өсімшесіне тең: dA=- dW_P . (3.6)

dA=Fdr болғандықтан, Fdr=-dW_P (3.7) түрінде жазуға болады. Осыдан W_P=-òFdr+С, мұндағы С-интегралдау тұрақты. Консервативті күштер үшін F_x= -дW_P/дx, F_у= -дW_P/ ду, F_z= -дW_P/ дz (3.8)

Немесе вектор түрінде F= - gradW_P (3.9)

мұндағы gradW_P =(дW_P/дx)i+(дW_P/ду)j + (дW_P/дz)k(3.10)

(i,j,k–координата осьтерінің бірлік векторлары). (3.10) өрнегімен анықталатын вектор W_P скалярының градиенті деп аталады. Ол gradW_P қатар ÑW_P белгіленуі де қолданылады.

Ñ («набла») Гамильтон операторыдеп аталатын символдық вектор немесе набла-оператор: Ñ=(дW_P/дx)i+(дW_P/ду)j + (дW_P/дz)k(3.11)

W_P функциясының түрі күш өрісінің сипатынан тәуелді болады. Мысалы, Жер бетінен h биіктіктегі массасы m дененің потенциалдық энергиясы:

W_P=mgh (3.12)

Серпімді деформацияланған дененің (серіппенің) потенциалдық энергиясын табайық. Серпімділік күші деформацияға пропорционал: F_x.сер=-kx

Мұндағы F_xсер-серпімділік күшінің х осіне проекциясы, k-серпімділік коэффициенті (серіппе үшін қатаңдық), минус таңбасы F_x.сер күштің бағыты деформация бағытына қарама-қарсы екендігін көрсетеді.

Ньютонның екінші заңы бойынша, деформация күші серпімділік күшіне модулі жағынан тең, ал бағытына қарама қарсы болады, яғни F_x =-F_x.сер=kx.

Аз ғана dx деформация жасайтын F_x күштің жасаған жұмысы:

_x dA=F_xdx=kxdx

Ал толық жұмыс A=ò kx dx=kx² /2

⁰

Сонда серпімді деформацияланған дененің потенциалдық энергиясы

W_P = kx² /2

Жүйенің толық энергиясы механикалық қозғалыс энергиясынан және өзара әсерлесу энергиясынан тұрады. W=W_P+W_к, яғни толық энергия потен-циалдық энергия мен кинетикалық энергияның қосындысынан тұрады.

Егер сыртқы диссипативті күштер әсер етпесе, онда d(W_P+W_к)=0. Осыдан W_P+W_к=W=const (3.13)

Ендеше, жүйенің толық механикалық энергиясы тұрақты болып қалады. Осы өрнек механикалық энергияның сақталу заңы болып табылады: өзара тек қана консервативті күштер әсер ететін жүйенің механикалық энергиясы сақталады, яңни уақыт өтуіне қарай өзгермейді.

Денелерге тек қана консервативті күштер (ішкі және сыртқы) әсер ететін механикалық жүйелер консервативті жүйлер деп аталады.Механикалық энергияның сақталу заңын келесі түрде тұжырымдауға болады: консервативті жүйелерде толық механикалық энергия сақталады.

Механикалық энергияның сақталу заңы уақыттың біртектілігімен байланысты.

Диссипативті жүйе деген жүйенің тағы да бір түрі бар, бұл жүйеде механикалық энергия энергияның басқа формасына (механикалық емес) өзгеру есебінен бірте-бірте кемиді. Бұл процесс энергия диссипациясы (немесе шашырау) деген атқа ие болды.