Электромагнетизм. Пример 1. Два параллельных бесконечно длинных провода D и С, по которым текут в одном направлении электрические токи силой I = 60 А

Пример 1. Два параллельных бесконечно длинных провода D и С, по которым текут в одном направлении электрические токи силой I = 60 А, расположены на расстоянии d = 10 см друг от друга.

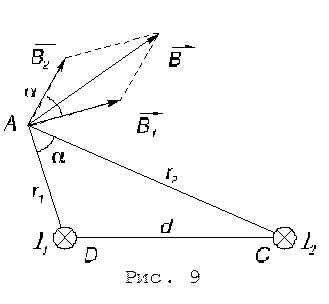
Определить индукцию 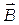магнитного поля, создаваемого проводниками с током в точке А (рис. 9), отстоящей от оси одного проводника на r₁ = 5 см, а от другого - на r₂ = 12 см.

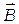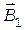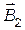Решение. Для нахождения магнитной индукции в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого выделим направление магнитных индукций и полей, создаваемых каждым проводником в отдельности, и сложим их геометрически: 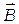= 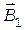+ 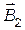(см. рис. 9).

Модуль вектора 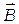может быть найден по теореме косинусов

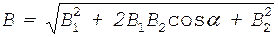, (1)

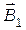
где a - угол между векторами и .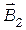

Магнитные индукции В₁ и B₂ выражаются соответственно через силу тока I и расстояния r₁ и r₂ от проводов до точки А:

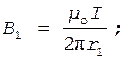
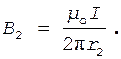
Подставляя выражения В₁ и B₂ в формулу (1) и вынося выражение 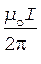за знак корня, получаем

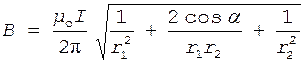. (2)

Вычислим cosa по теореме косинусов, учитывая, что Ð a = Ð DАС (как углы с соответственно перпен-дикулярными сторонами):

,

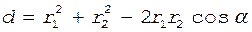где d - расстояние между проводами. Отсюда

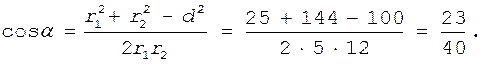
Подставим в формулу (2) числовые значения физических величин и произведем вычисления:

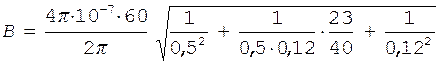= 309×10^-6 Тл =

= 309 мкТл.

Пример 2. Плоский квадратный контур со стороной а = 10 см, по которому течет ток силой I = 100 А, свободно установился в однородном магнитном поле (B = 1 Тл). Определить работу A, совершаемую внеш-ними силами при повороте контура относительно оси, проходящей через середину его противоположных сто-рон, на угол j=90°.

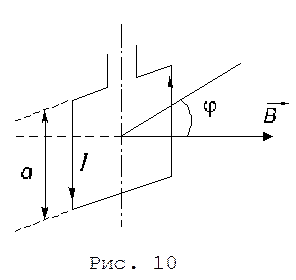
Решение. Работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока через контур (рис. 10):

A = -IDФ = I(Ф₁-Ф₂),

где Ф₁ - магнитный поток, пронизывающий контур до перемещения;

Ф₂ - магнитный поток, пронизывающий контур после перемещения.

Еслиj=90°, то Ф₁ = B×S, а Ф₂ = 0. Следовательно,

А = I×B×S = I×B×а² = 100×1×(0,1)² =1 Дж.

Примечание. Задача может быть решена другим способом, с использованием определения работы при вращательном движении:

А = МDj.

Предлагаем эти вычисления проделать самостоятельно и убедиться, что описанный выше способ решения задачи с использованием понятия магнитного потока более рационален.

Пример 3. В колебательном контуре, состоящем из индуктивности и емкости, максимальный ток в катушке равен I_m = 1 А, а максимальное напряжение на конденсаторе равно U_m = 1 кВ. С момента, когданапряжение равно нулю, до момента, когда энергия в катушке становится равной энергии в конденсаторе, проходит t = 1,56 мкс. Считая омическое сопротивление пренебрежимо малым, вычислить период колебаний контура и его энергию.

Решение. По условию задачи энергия магнитного поля в заданный момент времени равна энергии электрического поля в конденсаторе. Сумма этих энергий определяет полную энергию поля контура:

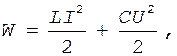
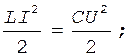(1)

где L - индуктивность контура;

I - ток в контуре;

С - емкость контура;

U - напряжение на пластинах.

Полная энергия контура, выраженная через максимальное напряжение, равна

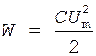. (2)

Из формул (1) и (2) определяем, что

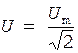. (3)

Используя уравнение гармонического колебания, в котором отсчет времени ведется от момента, когда напряжение равно нулю, имеем

,

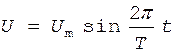где U_m - амплитуда напряжения (максимальное напряжение);

T - период колебаний;

t - время колебаний.

С учетом выражения (3) получаем

; .

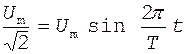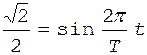Подставив числовые значения, находим Т:

,

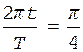откуда

.

Таким образом, период колебаний контура равен

Т = 8×1,57×10^-6 = 12,6×10^-6 с.

Вычислим теперь полную (максимальную) энергию контура. Она равна максимальной электрической энергии конденсатора (энергия магнитного поля при этом равна нулю) или максимальной энергии магнитного поля (при нулевой энергии электрического поля):

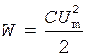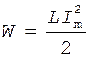, , (4)

где I_m - максимальный ток в катушке.

Используя формулу Томсона 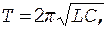получаем

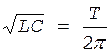. (5)

Произведение правых частей равенств (4) равно квадрату полной энергии контура 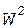. Извлечение корня с учетом формулы (5) дает

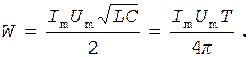
Вычисляем полную энергию контура:

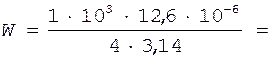0,001 Дж.

Пример 4. По двум параллельным проводникам, расположенным на расстоянии 20 см друг от друга, текут токи одного направления величиной в 100 А. Длина проводников равна 3 м. Вычислить силу взаимодействия между проводниками, если они находятся в вакууме.

Решение. На проводники с током в магнитном поле действует сила Ампера, которая может быть найдена по формуле

,

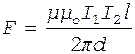где d - расстояние между проводниками;

l - их длина;

I₁ и I₂ - токи в проводниках;

m - магнитная проницаемость среды, равная для вакуума m = 1;

m_о - магнитная постоянная.

Подставив в формулу известные нам значения, получаем

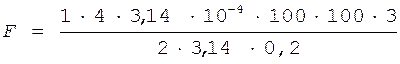= 0,03 Н.

Пример 5. Внутри длинного соленоида, имеющего однослойную обмотку из провода диаметром d = 1 мм, находится стальной сердечник. Определить магнитную проницаемость сердечника при силе тока, равной I = 2 А.

Решение. Индукция намагничивающего поля, т.е. поля внутри соленоида без сердечника, вычисляется по формуле

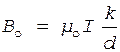, (1)

где k – число слоев обмотки.

Эта же индукция равна

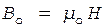, (2)

где Н – напряженность магнитного поля.

Из формул (1) и (2) следует, что

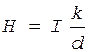. (3)

Если внутрь соленоида поместить сердечник с магнитной проницаемостью 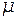, то индукция станет равной

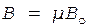. (4)

Отсюда с учетом соотношения (2) следует, что

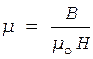. (5)

Подставляя в формулу (3) исходные данные, находим, что H = 2 кА/м, а затем по графику, изображенному на с.113 (см. приложение), для стали находим B = 1,25 Тл. Тогда

.

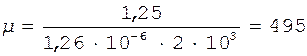Пример 6. Электрон, пройдя ускоряющую разность потенциалов, равную U = 400 В, попал в однородное магнитное поле напряженностью H = 1 кА/м.

Определить радиус кривизны траектории и частоту обращения электрона в магнитном поле, если вектор скорости перпендикулярен линиям поля.

Решение. На движущийся в магнитном поле электрон действует сила Лоренца, которая сообщает электрону нормальное ускорение. По второму закону Ньютона , где 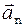- нормальное ускорение. Тогда в проекции на направление ускорения с учетом выражений для силы Лоренца и нормального ускорения имеем

,

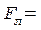
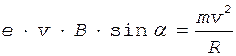где e - заряд электрона;

v - скорость электрона;

B - магнитная индукция;

m - масса электрона;

R - радиус кривизны траектории;

a - угол между векторам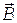и и 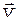(в нашем случае он равен 90°, следовательно, sin a = 1).

Отсюда найдем R:

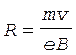. (1)

Если обозначить кинетическую энергию электронакак T, то входящий в равенство (1) импульс электрона mv может быть выражен как 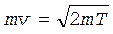. Используя равенство T = eU для определения кинетической энергии электрона, прошедшего ускоряющую разность потенциалов U, получаем

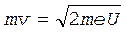. (2)

Магнитная индукция может быть выражена через напряженность H магнитного поля в вакууме как 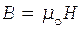. Подставив полученные выражения в формулу (1), находим

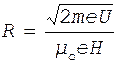. (3)

Производим вычисления:

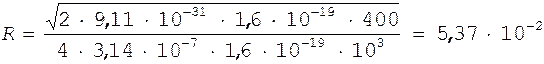м.

Частота обращения электрона в магнитном поле связана с его скоростью и радиусом соотношением 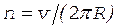. Подставив в это соотношение выражение (3) с учетом формулы(2), получаем

.

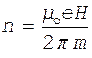Произведем вычисления:

c^-1 .

Пример 7.В однородном магнитном поле с индук-цией B = 0,1 Тл равномерно с частотой n = 10 об/c вращается рамка, содержащая N = 1000 витков, плотно прилегающих друг к другу. Площадь рамки равна S = 150 см². Определить мгновенное значение ЭДС индукции в момент времени, когда угол поворота рамки равен .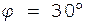

Решение. Мгновенное значение ЭДС индукции определяется уравнением Фарадея - Максвелла

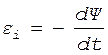, (1)

где 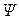- потокосцепление, связанное с магнитным потоком Ф и числом витков N соотношением

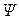= NФ.(2)

Подставляя выражение (2) в формулу (1), получаем

.

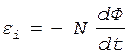При вращении рамки магнитный поток, пронизывающий ее в момент времени t, определяется соотношением

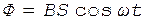, (3)

где B - магнитная индукция;

S - площадь рамки;

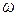- циклическая частота.

Подставив в формулу (2) выражение (3) и продиф-ференцировав по времени, найдем мгновенное зна-чение ЭДС индукции:

.

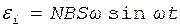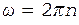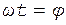Учитывая, что , а , получаем

.

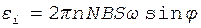Произведем вычисления:

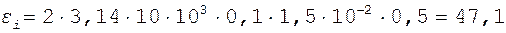B.

Пример 8.Имеется катушка, индуктивность кото-рой равна L = 0,2 Гн, а сопротивление R = 1,64 Ом.

Найти, во сколько раз уменьшится сила тока в катушке через t = 0,05 с после того, как катушка отключена от источника тока и замкнута накоротко.

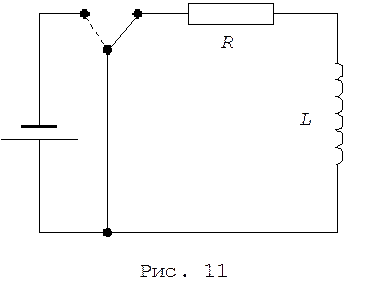
Решение. При выключении тока в цепи, содержащей R и L (рис. 11), и ²закорачивании² катушки ток в ней изменяется по закону

,

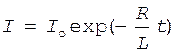где I_о - значение тока до ²закорачивания² катушки.

Через промежуток времени t₁ сила тока в катушке будет равна 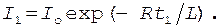Тогда отношение токов будет следующим:

.

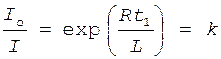Произведем вычисления:

раза.