ЭФФЕКТ КОМПТОНА

Дальнейшее обоснование дискретности электромагнитного излучения было получено в экспериментах А.Комптона в 1922 году. Обнаруженный в этих опытах эффект состоит в следующем. При прохождении монохроматического рентгеновского излучения через вещество наряду с излучением исходной длины волны 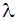(частоты 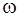) наблюдается рассеянное под углом 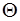излучение другой длины волны, причем разность длин волн Dl=(l¢-l) не зависит от длины волны l и природы рассеивающего вещества, а зависит лишь от угла рассеяния Q :

Dl=l_c (1 - cosQ), (1.43)

где l_с - комптоновская длина волны электрона:

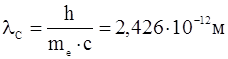, (m_e – масса электрона).

Классическая электродинамика не дает объяснения Комптон-эффекту. Однако его легко объяснить, допустив, что рентгеновское излучение состоит из фотонов.

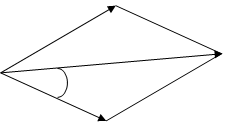
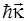Отдельный фотон с энергией и импульсом сталкивается со слабо связанным (квазисвободным) электроном вещества по законам упругого удара (рис.1.10).

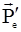
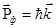
Q

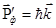
Рис.1.10

Применим к этому процессу закон сохранения энергии (1.33) и импульса (1.34):

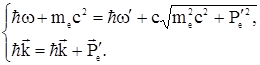(1.44)

(1.45)

где 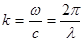- волновое число.

Закон сохранения энергии (1.44) записан в релятивистской форме, поскольку электрон после соударения может приобрести скорость, соизмеримую со скоростью света в вакууме.

Здесь предполагается, что до соударения импульс электрона = 0, а после соударения электрон получает лишь часть энергии фотона, (в отличие от фотоэффекта, где фотон отдает связанному электрону всю энергию). После несложных преобразований уравнений (1.44) и (1.45), можно прийти к формуле (1.43), установленной экспериментально, или к формуле

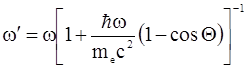. (1.46)

Нетрудно видеть, что при 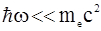справедлив результат классической физики: w¢=w или (Dl®0). Иначе говоря, в предельном случае “мишень” столь массивна, что “не чувствует“ корпускулярного характера излучения. Это объясняет наличие в составе рассеянного излучения волн исходной частоты: часть фотонов рассеивается на электронах, которые сильно связаны с атомом (внутренние электроны). При этом обмен энергией и импульсом происходит с атомом как целым, и под l_с в формуле (1.43) следует понимать комптоновскую длину волны атома, то есть (масса атома М_а<<m_е, поэтому Dl®0).

Формулы (1.43), (1.46) были подтверждены при рассеянии на парафине, графите и других веществах.