ФОТОЭФФЕКТ
Согласно классической теории электромагнитного поля Максвелла, энергия W электромагнитного излучения, заключенного в некотором объеме V, определяется средним квадратом амплитуды напряженности Е электрического поля:
W ~ < Е2 > · V~I· V, (1.35)
где I – интенсивность электромагнитной волны, способная принимать любые, сколь угодно малые значения.
Это следствие теории Максвелла полностью подтверждается многочисленными экспериментами. Первым указанием на то, что это не всегда так, явился открытый Г.Герцем в 1887 г. фотоэффект.
Различают фотоэффект внешний, внутренний и вентильный.
Внутренний фотоэффект – перераспределение электронов вещества по энергетическим состояниям при поглощении электромагнитного излучения. В полупроводниках и диэлектриках это проявляется в изменении электропроводности и диэлектрической проницаемости этих материалов или в возникновении фото-э.д.с. В металлах из-за их высокой электропроводности внутренний фотоэффект неощутим.
Вентильный фотоэффект – это разновидность внутреннего фотоэффекта – возникновение фото-э.д.с. при освещении контакта двух разных материалов (полупроводников или полупроводника и металла).
Внешний фотоэффект – фотоэлектронная эмиссия - испускание электронов (в вакуум или другую среду) твердыми телами и жидкостями под действием электромагнитного излучения.
Первые систематические исследования внешнего фотоэффекта провел А.Г.Столетов в 1888-1889гг.
На рис.1.6 приведена принципиальная схема включения вакуумного фотоэлемента (ФЭ) для изучения закономерностей внешнего фотоэффекта.
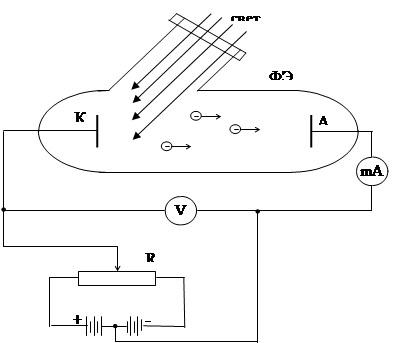 |
Рис.1.6
Через кварцевое окошко монохроматический свет освещает катод К из исследуемого материала. Под действием электрического поля вырванные из катода электроны (фотоэлектроны) перемещаются в вакуумной трубке ФЭ к аноду А. Интенсивность фотоэффекта оценивается по силе фототокаIф, измеряемого миллиамперметром (или гальванометром). Напряжение U между анодом и катодом можно регулировать потенциометром R и измерять вольтметром.
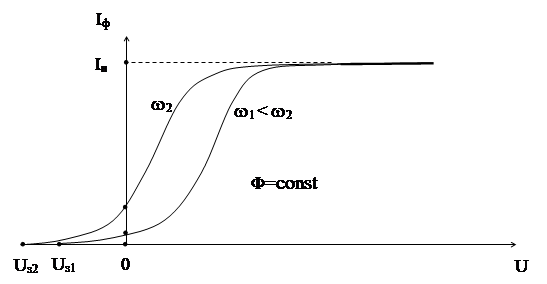
 Вольт-амперные характеристики фотоэффекта, соответствующие двум значениям светового потока Ф, падающего на катод, приведены на рис.1.7 (частота света w в обоих случаях одинакова).
Вольт-амперные характеристики фотоэффекта, соответствующие двум значениям светового потока Ф, падающего на катод, приведены на рис.1.7 (частота света w в обоих случаях одинакова).
Рис.1.7
Фототок возникает практически мгновенно вслед за включением источника. По мере увеличения U фототок постепенно нарастает, т.е. все большее число фотоэлектронов достигает анода. Пологий характер кривых показывает, что электроны вылетают из катода с разными по величине скоростями. При U= 0 лишь часть электронов, обладающих достаточно большой энергией, достигает анода (ток Io - мал). Максимальное значение фототока – Iн (фототок насыщения) – определяется таким значением U, при котором все электроны, испускаемые катодом, попадают на анод:
Iн=еn,
где n – число фотоэлектронов в 1 с.
Чем больше световой поток Ф (или интенсивность света), тем больше n и, следовательно, тем больше ток насыщения Iн.
Если приложить достаточное по величине отрицательное напряжение Uз - задерживающее напряжение, то фототок обращается в нуль. При таком напряжении даже самому высокоэнергетичному фотоэлектрону не удается преодолеть задерживающее поле и достичь анода. Следовательно, можно записать, что
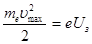 , (1.36)
, (1.36)
где mе, e, umax - масса, заряд и максимальная начальная скорость электрона. Различным световым потокам соответствует (при w=соnst) одно и то же Uз.
 Эксперимент показывает, что большей частоте падающего на катод света соответствует большее задерживающее напряжение Uз, то есть большая кинетическая энергия Wk испущенных электронов (см.рис.1.8). Кроме того, Uз зависит от материала катода.
Эксперимент показывает, что большей частоте падающего на катод света соответствует большее задерживающее напряжение Uз, то есть большая кинетическая энергия Wk испущенных электронов (см.рис.1.8). Кроме того, Uз зависит от материала катода.
Рис.1.8
При обобщении экспериментальных данных были установлены три закона внешнего фотоэффекта.
1. Закон Столетова: при неизменном спектральном составе излучения, падающего на фотокатод, число электронов, вырываемых из катода в единицу времени, пропорционально интенсивности излучения, то есть сила фототока насыщения пропорциональна световому потоку:
Iн= gфФ,
где gф - интегральная чувствительность фотоэлемента.
2. Максимальная начальная кинетическая энергия фотоэлектронов, выбиваемых с катода, пропорциональна частоте w света (см.рис. 1.8) и не зависит от интенсивности светового потока.
3. Для каждого вещества существует “красная граница” фотоэффекта, т.е. такая минимальная частота wо света (см.рис.1.9), ниже которой фотоэффект невозможен при любой интенсивности света (wо зависит от химической природы вещества и состояния его поверхности).
Классическая электродинамика оказалась не способной объяснить вышеизложенные закономерности. В этой теории свет рассматривается как электромагнитная волна. Взаимодействуя с полем волны, электрон должен набирать энергию Wk, пропорциональную интенсивности света (см.формулу (1.35)) и не зависящую от частоты. Поэтому свет любой частоты, но достаточно большой интенсивности (I ~ Ф) должен был бы вырывать электроны из металла. Кроме того, волновая теория не смогла объяснить безинерционность фотоэффекта, установленную экспериментально. Если же принять гипотезу Эйнштейна о том, что свет – это совокупность фотонов, то явление фотоэффекта легко объясняется.
 |
Р
Рис.1.9
По мысли Эйнштейна взаимодействие фотона с электроном внутри металла сводится к мгновенному поглощению всей энергии фотона одним электроном. Именно поэтому, число вырванных фотоэлектронов пропорционально числу фотонов, падающих на катод фотоэлемента в единицу времени, то есть световому потоку (первый закон фотоэффекта).
Воспользуемся законом сохранения энергии (1.33). Полагая 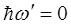 (фотон после взаимодействия перестает существовать, т.к. полностью поглощается), получим
(фотон после взаимодействия перестает существовать, т.к. полностью поглощается), получим
 . (1.37)
. (1.37)
Энергия W электрона внутри металла отрицательна (энергия притяжения). Чтобы покинуть металл, он должен получить энергию, достаточную для совершения работы против сил притяжения – работы выхода, поэтому
Aвых = – W. (1.38)
Вылет электрона наблюдается, если 
 .
.
Энергия W¢ в (1.37) – это начальная кинетическая энергия электрона после выхода из металла, то есть
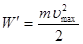 . (1.39)
. (1.39)
Подстановка выражений (1.38) и (1.39) в формулу (1.37) приводит к известной формуле Эйнштейна для внешнего фотоэффекта, прекрасно согласующейся с экспериментом:
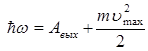 . (1.40)
. (1.40)
Таким образом, энергия  поглощенного фотона расходуется на совершение электроном работы выхода
поглощенного фотона расходуется на совершение электроном работы выхода  и на сообщение вылетевшему фотоэлектрону кинетической энергии.
и на сообщение вылетевшему фотоэлектрону кинетической энергии.
В частности, из формулы (1.40) вытекает существование красной границы фотоэффекта, то есть такой частоты wо, при которой 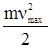 = 0:
= 0:
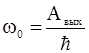 . ( 1.41)
. ( 1.41)
Используя формулы (1.36) и (1.41) можно записать уравнение (1.40) в виде
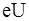 3
3 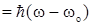 , (1.42)
, (1.42)
из которого следует линейная зависимость задерживающего напряжения от частоты света (рис.1.9).
В случае очень большой интенсивности света (лазерные пучки) возможен многофотонный фотоэффект, при котором электрон может поглотить сразу несколько фотонов . Уравнение Эйнштейна для многофотонного фотоэффекта имеет вид:
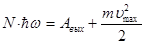 .
.
Дата добавления: 2015-07-24; просмотров: 1545;
