Пример расчета опционной операции
| Инвестор приобретает американский опцион coll на лот базового актива Х за 250 руб. | E =50 руб. Размер лота = 100 шт. Общая сумма исполнения опциона, т. о. 5000 руб. |
| Определим, как должна измениться цена базового актива, чтобы инвестор не понес убытков. Приобретатель опциона сoll заинтересован в росте цены базового актива выше цены исполнения. | Определим стоимость опциона на 1 ценную бумагу: V0coll* = 250/100 = 2.5 руб. Минимальное изменение цены Х, чтобы исключить потери инвестора, т. о. составит: Pminобосн. = 50 + 2,5=52,5 руб. |
| Определим доходность по опциону, если цена Х вырастет до 60 руб. | Реализуя опцион, инвестор получает: 60 * 100 – 50*100 – 250 = 750 руб. Т. о. Доходность по опциону в этом случае составит 750/250*100% = 300%. |
| Определим убытки инвестора, если цена опциона упадет до 40 руб. | При цене Х=40 реализация опциона нецелесообразна, т. о. убытки инвестора будут равны стоимости опциона = 250 руб. |
| При росте цены Х лишь до 52руб. с целью минимизации потерь инвестор реализует опцион. | 52*100-50*100-250 = -50 руб. (убыток) |
Таблица 1.6
| Расчет стоимости опциона по биномиальной модели Блэка-Шоулеса (используется для европейских опционов) | |
| Стоимость coll-опциона представляется эквивалентом репликантного портфеля | Репликантный портфель представляет собой заем определенной суммы средств по безрисковой ставке и покупку некоторого количества базового актива (акции) |
| Простая биномиальная модель предполагает, что в момент окончания опциона основная акция имеет одну из двух возможных цен, одна из которых принесет владельцу опциона прибыль (Z), а другая сделает реализацию опциона нецелесообразной. |  ,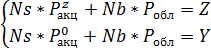
Где:
Pобл – стоимость облигации в момент исполнения опциона;
Pакцz – стоимость акции, обеспечивающая целесообразность реализации опциона;
Ns – количество акций в портфеле;
Nb – количество облигаций в портфеле.
Y – стоимость опциона, когда его реализация нецелесообразна, равна 0, если реализация опциона целесообразна, то уравнение будет обеспечивать расчетную прибыль.
|
| Стоимость облигации с учетом временной стоимости денег и при заданной безрисковой ставке доходности определяется по формуле. |  ,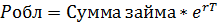
где:
e - математическая константа, основание натурального логарифма;
r – безрисковая ставка процента.
|
| Решая систему уравнений можно рассчитать количество акций и облигаций в портфеле. Таким образом, цена опциона coll (Vocoll) составит |  ,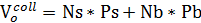
где:
Ps – первоначальная стоимость базового актива (акции);
Pb – первоначальная стоимость облигации;
В репликантном портфеле Pb принимается равной по размеру Ps
|
| Таким образом, чтобы сформировать репликантный портфель инвестор должен занять определенную сумму денег и с ее помощью приобрести необходимое количество базового актива (акций). Количество акций необходимых, чтобы заменить один опцион на покупку, называется коэффициентом хеджирования или опционной дельтой (h) |
|
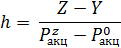
| Сумма средств (B), которые необходимо занять по безрисковой ставке для приобретения h акций (базового актива) определяется по формуле |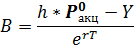 
|
| Исходя из представленных расчетов, формулу стоимости опциона на покупку можно представить и в следующем виде |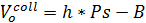 
|
Стоимость опциона на продажу рассчитывается исходя из фундаментальной взаимосвязи опционов.
Учитывая, что (h-1)<0, можно говорить, что репликантный портфель для опциона на продажу стоится путем короткой продажи (1-h) акции и инвестирования в безрисковую облигацию суммы  .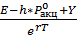
| 
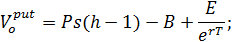или
|
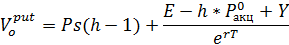
Таблица 1.7
Дата добавления: 2015-07-24; просмотров: 895;