Сущность эффекта и экономической эффективности.
Осн. целями хоз. деят-ти в условиях рыночной эк-ки явл. получение произв. прибыли, достаточной для его расширенного воспр-ва, роста материального благосостояния его работников и пополнения бюджетов всех уровней.
Достижение этих целей связано с разработкой инвестиционных проектов, под кот. понимают комплексный план мероприятий, включающий кап. строительство, приобретение технологий и оборудования, подготовку кадров и т.д., направленных на создание нового или модернизацию действующего пр-ва товаров и услуг с целью получения прибыли.
Прибыльность инвестиционного проекта определяется как норма прибыли на инвестиции.
Кап. вложения осуществляются только в том случае, если прибыль от них достигает определенного заранее задаваемого минимума.
При этом в качестве альтернативы рассматривается вложение средств в др. проекты, в ценные бумаги или помещение их в банк под определенный процент.
Т.к. одни и те же хоз. задачи могут решаться несколькими вариантами, различающимися по величине затрат и срокам их реал-ии, то необходим выбор наиболее экономичного, эффективного.
При этом необходимо сопоставить две величины: рез-т от внедрения какого-то варианта в пр-во и затраты на внедрение этого варианта. Их соотношение и предст. собой эконом. эффективность затрат, кот. в общем виде выражается формулой
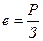 , где
, где
е – эффективность затрат,
Р – результат от внедрения варианта.
З – затраты на его внедрение.
Э = (Р – З) – эффект, т.е.
Показатель полезности, позволяющий судить о том, что получает общество.
Он может быть как экономическим, так и социальным, научным, научно-техническим.
Эффективность позволяет судить о том, какой ценой, какими затратами достигнут этот эффект.
Если необходимо определить общую отдачу от инвестиций без сравнения с др. вариантами, т.е. ответить на вопросы «Что делать?», «Делать или не делать?», «Эффективно или неэффективно?», тогда рассчитывают абсолютную (общую) эффективность в виде:
1. рентабельности кап. вложений как отношение годовой прибыли к сумме инвестиций:
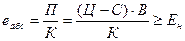
П – годовая прибыль от вложения инвестиций
Ц – оптовая цена ед. продукции
С – с/с ед. продукции
В – годовой выпуск этой продукции
К – сумма полных инвестиций или кап. вложений.
2. если предлагаются мерприятия, приводящие к снижению с/с продукции, то
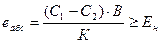
С1 и С2 – с/с ед. продукции соотвественно до и после внедрения мероприятия.
Рассчитанные значения еабс сравнивают с нормативом Ен и кап. вложения признаются экономически эффективными, если еабс не ниже Ен.
Ен – показывает норму прибыли, кот. должна быть получена на 1 руб. инвестиций (1 формула) или величину снижения с/с ед. продукции на 1 руб. инвестиций (2 формула).
Наряду с показателями эффективности исп-ют и показатель срока окупаемости полных кап. вложений, кот. показывает время. В течение кот. полные кап. вложения окупятся либо прибылью, либо снижением с/с от внедрения мероприятия.
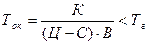
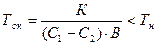
Абсолютная связь между эффективностью и Ток:
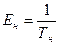 ;
; 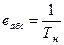
Рассчитанное значения срока окупаемости необходимо сравнить с нормативным его значением и инвестиции признаются целесообразными, если Ток<Тн.
До перехода к рыночной эк-ке Ен и Тн устанавливались вышестоящим органом управления.
В настоящее время каждое пред-ие устанавливает для себя самостоятельно приемлемый уровень кап. вложений, кот. обеспечит ему нормальный размер прибыли.
Американский экономист Хонко приводит типичное для американских и европейских пред-ий разделение кап. вложений на классы и размер Ен для них:
1. вынужденные кап. вложения, кот. осуществляются с целью повышения надежности пр-ва, техники безопасности, охраны окружающей среды. В этих случаях нет выбора между инвестировать или нет, и, → требования к норме прибыли отсутствуют.
2. Кап. вложения для сохранения позиций пред-ия на рынке и поддержания его репутации.
Ен = 6%, т.е. Ен = 0,06
3. Кап. вложения на обновление ОПФ особого оборудования
Ен = 12%; Ен = 0,12.
4. Кап. вложения на экономию затрат, т.е. снижения с/с и повышения прибыли, а также на повышение производительности труда.
Ен = 15%, Ен = 0,15.
5. Кап. вложения, направленные на увеличение произв. мощностей пред-ия.
Ен = 20%, Ен = 0,2.
6. Рисковые кап. вложения, направленные на новое строительство, разработку новых видов продукции, новых технологий, освоение новых сегментов рынка.
Ен = 25%, Ен = 0,25.
Нижняя граница нормы прибыли хар-ет тот минимальный уровень, ниже кот. норма прибыли не должна падать независимо от того, каковы фин. ресурсы пред-ия и ожидаемый размер прибыли от проекта.
В среднем по мировому опыту при стабильных условиях рыночной эк-ки Ен составляет 15%, или 0,15.
На эту величину будем ориентироваться в расчетах, однако выбор ее определяется источником инвестирования.
1. Если это собственные средства, то Ен может быть и ниже 15%.
2. Если это ассигнование, то не ниже 0,15.
3. Если же это заемные средства, то Ен не ниже банковской ставки % за кредит.
Т.о., если Ен = 0,15, то 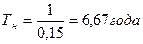
Если же необходимо ответить на вопрос «Как делать?», «Какой вариант технологии или орг-ии пр-ва лучше?», тогда рассчитывают сравнительную (относительную) эконом. эффективность инвестиций, для чего исп-ют показатели сравнительного эффекта и сравнительной экономической эффективности, кот. в общем виде рассчитываются:
 ,
, 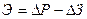 ,
,
∆Р – дополнительный рез-т от внедрения более капиталоемкого варианта.
∆З – дополнительные затраты по тому варианту.
Как правило, из сравниваемых вариантов у одного выше с/с, но ниже кап. вложения, поэтому выбор лучше осуществить с помощью системы показателей:
1. Сравнительная (относительная) эффективность кап. вложений.
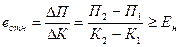
∆П = П2 – П1 – прирост прибыли по более капиталоемкому варианту
∆К – дополнительные кап. вложения у более капиталоемкого варианта.
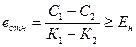
2. Срок окупаемости дополнительных кап. вложений:

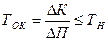
3. Минимум приведенных затрат
Зi = Ci + Eн · Ki → min
Сi - с/с ед. продукции или годовая i-того варианта
Кi – удельные или полные кап. вложения i-того варианта.
Зная, что Ен = 1/Тн и подставив в Зi, получим формулу:
Зi = Ki + Tн · Ci → min
Если число сравниваемых вариантов больше 2-х, то наряду с выбором оптимального варианта min приведенных затрат можно исп-ть и цепной ме6тод сравнения, когда в качестве осн. формулы выбирают либо сравнительную эффективность, либо срок окупаемости и по ним сравнивают 2 др. варианта. Лучший из них сравнивается с 3-м и т.д. до тех пор пока останется 1 оптимальный вариант.
Например: Представлено 3 варианта новой техники:
| Показатели | I | II | III |
| c/c годового объема, млн. руб. | |||
| полные кап. вложения, млн. руб. |
Выбрать лучший цепным методом.
е1-2 = (20-14)/(300-250) = 6/50 = 0,12 ≤ Ен
е = ∆Р/∆З = 6/50 ≥ Ен
Т.к. 0,12 < Ен, то II вариант хуже, несмотря на то, что с/с ниже, затраты у него выше на 50 млн. руб.
е1-3 = (20-12)/(350-250) = 8/100 = 0,08 ≤ Ен
снижать с/с невыгодно, т.к. 0,08 < Ен
2-й метод.
З1 = 20 + 0,15 · 250 = 47,5 (лучший)
З2 = 14 + 0,15 · 300 = 59
З3 = 12 + 0,15 · 350 = 64,5.
После того, как по 1-му из этих методов выбран лучший вариант, рассчитывается годовой эконом. эффект от его внедрения как разность приведенных затрат.
Э = З1 – З2
Э1-2 = 59 – 47,5 = 11,5 млн. руб.
Э1-3 = 64,5 – 47,5 = 17 млн. руб.
Учет фактора времени при выборе оптимального варианта
Одна из главных проблем при расчете инвестиций состоит в том, чтобы сопоставить выплаты, кот. делаются в разные моменты времени. Одинаковые по величине, но осуществляемые в разное время затраты экономически неравноценны.
В условиях рыночной эк-ки при проведении фин. операций, связанных с долгосрочными вложениями средств, особую роль играет фактор времени.
Золотое правило бизнеса гласит: сумма, полученная сегодня, больше той же суммы, полученной завтра, на величину приносимой ею прибыли.
Вы обладаете суммой в 10 тыс. руб., кот. помещаете в банк на депозит (вклад) под 10% годовых. В идеальном случае при отсутствии инфляции, соотв. налогообложения, риска неплатежеспособности банка через 1 год вы будете иметь сумму 10000 (1 + 0,1) = 11000, доход 1000 руб.
Вы хотели бы через год иметь 10 тыс. руб. Сколько нужно положить сегодня в банк?
х (1 + 0,1) = 10000
10000 /(1 + 0,1) = х = 9091, доход составляет 909 руб (10000 – 9091 = 909)
т.о., 10 тыс. сегодня равноценны 11 тыс. завтра, но 10 тыс. завтра равноценны 9091 руб. сегодня. Неравноценность 2-х одинаковых по величине, но разных по времени получения сумм вызваны след. причинами:
1. сегодняшние деньги обладают большей ценностью, чем будущие, т.к. они могут быть немедленно инвестированы и начать приносить доход.
2. в условиях даже небольшой инфляции покупательная способность денег со временем снижается.
3. отдается предпочтение текущему потреблению, чем будущему.
В связи с этим необходимо учитывать фактор времени при проведении фин. операций, связанных с долгосрочными кап. вложениями.
Для учета фактора времени исп-ют 2 метода:
1. Метод наращения (компаудинг)
2. Метод дисконтирования.
При этом важную роль играет используемая ставка %, кот. рассматривают в качестве нормы доходности фин. операции.
Под наращением (компаудингом) понимают процесс увеличения первоначальной суммы в рез-те накопления %, т.е. в рез-те начисления сложных %.
Этот метод исп-ся для определения будущей наращенной величины денежной суммы.
Например:
Сумма в 10 тыс. руб. хранилась на депозите в банке в течение 3-х лет при банковской ставке 10% годовых. Какова она будет через 3 года?
Через год: 10000(1 + 0,1) = 11000
Через 2 года: 10000(1 + 0,1) · (1 + 0,1) = 10000(1 + е)2
Через 3 года: 10000(1 + е)3 = 13310 руб.
Т.о., если обозначить будущую стоимость FV – future value, настоящую (текущую) – PV – present value, число лет осуществления операции обозначить через t (у нас три года), норму доходности операций через Е и она равна ставке % за кредит (10%), то
FV = PV(1 + E)t
Kt = K0(1 + E)t
α = (1 + E)t –
коэффициент наращения, или коэффициент начисления сложных процентов.
В фин. практике часто сталкиваются с задачей, обратной определению наращенной суммы, т.е. по известной в будущем стоимости FV необходимо определить будущую стоимость PV. Тогда говорят, что сумма FV дисконтируется.
Т.о., дисконтирование – это определение текущей стоимости денежной величины по ее известному значению в будущем исходя из заданной ставки %.
Если при наращении денежная сумма приводится к концу анализируемого периода, то при дисконтировании разновременные показатели приводятся к их стоимости в начальном периоде, т.е.
tначальное = 0 (tрасч = 0)
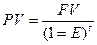
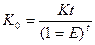
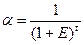 -
-
дисконтный множитель, или коэффициент дисконтирования.
Например:
Определить сумму, кот. будучи положенной на депозит соком на 4 года под 10% годовых, составит в конце периода 14641 руб.
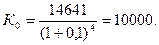
если % начисляются не 1 раз в год, а несколько (например, раз в месяц, квартал, полгода), то эти формулы видоизменяются:
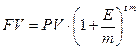
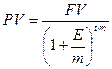
m – число раз начисления % в году.
Вышеуказанными формулами пользуются, если денежный поток осуществляется в виде разовых платежей.
Большинство же фин. операций предст. собой денежный поток в виде серии равных или произвольных по величине платежей, распределенных во времени. Денежные потоки, состоящие из периодически равных по величине платежей, наз. обыкновенными аннуитетами, т.е. фин. рентой.
Будущая стоимость обыкновенного аннуитета предст. собой сумму всех составляющих его платежей с начисленными на них % на конец совершения операции.
FVt = P1· (1+E)t-1 + P2· (1+E)t-2 + … +Pt · (1+E)t-t
В свернутом виде эта формула:
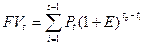
t – расчетный год или год приведения расчетных затрат (последний год сверешния операции)
Р1, Р2, Рt – это платежи в 1-м, 2-м и году t.
tp = t (в данном случае)
ti – рассматриваемый год.
Ежегодно в банк вносится 10000 руб. под 10% годовых. Какова она будет к концу 4-го года?
FVt = 10000 · (1 + 0,1)4-1 + 10000 · (1 + 0,1)4-2 + 10000 · (1 + 0,1)4-3 + 10000 · 1 = 46410 руб.
Текущая стоимость обыкновенного аннуитета есть сумма всех составляющих его платежей, дисконтированных на момент начала операции.
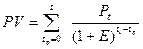
Например:
Мы хотим ежегодно получать доход 10000 руб. Какова должна быть сумма, положенная в банк сегодня, чтобы обеспечить такой доход, если банковская ставка 10% годовых?
PV = 10000 · 1/(1+0,1)1-0 + 10000 · 1/(1 + 0,1)2-0 + 10000 · 1/(1 + 0,1)3-0 + 10000 · 1/(1 + 0,1)4-0 = 31600 руб.
Будущая (наращенная) стоимость и текущая соимось аннуитетов с произв. платежами определяется аналогично аннуитетам с одинаковыми платежами, только Pt и Pi заменяются на Кt и Кi .
При анализе инвестиций и выборе их оптимального варианта необходимо сопоставлять затраты и доходы, возникающие в разное время, т.е. учитывать, что затраты на осуществление проекта растягиваются во времени, а доходы от реал-ии проекта, помимо того, чо они тоже растягиваются по времени, еще и возникают после осуществления затрат.
В этом случае также учитывают фактор времени с помощью компаудинга или дисконтирования, т.е. и доходы от реал-ии проекта (прибыль) и инвестиции на реал-ию проекта приводят к одному расчетному году, кот. может быть либо началом инвестирования (Трасч = 0), или концом инвестирования (последний год вложения инвестиций или предшествующий началу реал-ии продукции).
Основным показателем эффективности инвестиций в этом случае явл:
ЧДД – чистый дисконтированный доход
Iп – индекс прибыльности
ВНД – внутренняя норма доходности
Токуп-ти – срок окупаемости инвестиций.
I. ЧДД (чистая приведенная стоимость, чистая текущая стоимость, NPV – net present value)
Основная идея ЧДД заключается в том, чтобы по заданной величине дисконта Е определить текущую стоимость всех оттоков и притоков денежных средств в течение всего жизненного цикла и сопоставить их друг с другом.
Пусть:
К – первоначальные инвестиции, т.е. сумма инвестиций на начало проекта)
PV – текущая стоимость чистого дохода проекта (прибыли) на протяжении всего жизненного цикла проекта.
Тогда в общем виде ЧДД рассчитывается:
ЧДД = PV – К
В более широком представлении при разовых первоначальных инвестициях ЧДД рассчитывается:
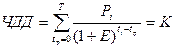
Если же инвестиции распределены по годам, то ЧДД =
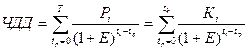 , где
, где
tp = 0 – это расчетный год или год приведения разновременных денежных сумм к началу инвестирования.
Т – жизненный цикл проекта, т.е. время от зарождения идеи с учетом научных исследований самой реконструкции или расширения пр-ва, оптового и массового пр-ва продукции до нормального старения продукции и снятия ее с пр-ва или морального и физического старения оборудования и его реновации.
Pi – чистая прибыль от реал-ии в i-том году, определяемая как разность между выручкой от реал-ии и текущими затратами на пр-во, т.е. себестоимостью.
Ki – кап. вложения в i-том году
Е – норма дисконта
ti – рассматриваемый год
tk – последний год инвестирования.
Если рассчитанный по этим формулам ЧДД > 0, это означает, что в течение своего жизненного цикла Т проект возместит первоначальные инвестиции К, обеспечит получение прибыли согласно заданному стандарту Е, а также ее некоторый резервный ЧДД.
Если ЧДД < 0, то это говорит о том, что заданная норма прибыли Е не обеспечивается, а проект явл. убыточным.
Если ЧДД = 0, то проект только окупает заданные затраты, но не приносит прибыль.
Пример 1. Имеется инвестиционный проект с общей суммой инвестиций 250 млн. руб., распределенной по годам. После ввода в действие проекта ежегодные поступления:
| Вариант | Инвестиции, млн. руб. | Прибыль, млн. руб. | ||||
| А |
Ставка дисконтирования 10% годовых.
Рассчитать все показатели эффективности инвестиций.
Дисконтируем инвестиции (приводим к tp = 0).
100/(1 + 0,1)1 + 150/(1 + 0,1)2 = 214,88 млн. руб.
дисконтируем доходы:
50/(1 + 0,1)3 + 150/(1 + 0,1)4 + 200/(1 + 0,1)5 + 200/1,16 = 377,1 млн. руб.
ЧДД = 377,1 – 214,88 = 162,27 млн. руб.
ЧДД – абсолютный показатель эффективности инвестиций, однако если из 2-х вариантов он одинаков, то выбрать лучший вариант сложно.
Пример 2.
| Проект | К | PV | ЧДД |
| А | |||
| Б |
В этом случае используют относительные показатели эффективности инвестиций, такие, как индекс прибыльности и внутренняя норма доходности.
II. Iп – доходности, рентабельности проекта. Показывает, сколько денежных единиц текущей стоимости будущего денежного потока приходится на одну денежную единицу инвестиций.
Если инвестиции разовые, то
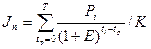 , руб/руб или · 100%
, руб/руб или · 100%
Если инвестиции распределены по годам, то
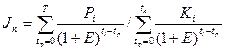 ,
,
Индекс прибыльности Iп хар-ет эффективность инвестиций, а также некоторую дополнительную рентабельность, т.к. при ее расчете и доходы и инвестиции уже дисконтированы по ставке Е.
Если Iп = 1, это означает, что доходность инвестиций точно соответствует нормативу рентабельности, т.е. ставке дисконта Е.
Если Iп < 1, то инвестиции нерентабельны, т.к. не обеспечивают этот норматив Е.
Если Iп > 1, то текущая стоимость денежного потока доходов проекта превышает первоначальные инвестиции, превышая тем самым положительное значение Е. (см. пример 3 далее).
 Пример 3.
Пример 3.
А = 150000 : 10000 = 1,5 руб/руб
В = 105000 : 100000 = 1,05 руб/руб → вариант А лучше.
Вернемся к самому первому проекту.
Iп = 377,1 : 214,88 = 1,75 руб/руб.
III. ВНД – внутренняя норма доходности (IRR – internet rate of return).
Под ВНД понимают расчетную ставку %, при кот. получаемые доходы от реал-ии проекта становятся равными затратам на проект, т.е. ВНД – это такая расчетная ставка %-ов, при кот. величина приведенных доходов равна приведенным на эту же дату инвестициям и → ЧДД = 0.
Если расчет ЧДД инвестиционного проекта дает ответ на вопрос, явл. ли он эффективным или нет при некоторой заданной норме дисконта Е, то ВНД проекта определяется в процессе расчета и затем сравнивается с требуемой инвестором нормой дохода на вкладываемый капитал.
Если инвестиции разовые, то ВНД определяется из условия
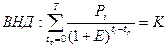
Если инвестиции распределяются по годам, то
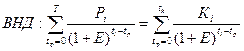
Если инвестиции осуществляются за счет привлеченных или заемных средств, причем кредит получен по ставке Е, то «ВНД – Е» показывает эффект инвестиционной деят-ти, → ВНД должен быть > ставки ссудного процента за кредит.
При ВНД = Е доход только окупает инвестиции, но они бесприбыльны.
При ВНД < Е инвестиции убыточны.
ВНД можно рассчитать по формуле
 , где
, где
Е1 – ставка дисконта (%), при кот. ЧДД положителен.
Е2 – ставка дисконта (%), при кот. ЧДД отрицателен.
Пример. Определить ВНД проекта, если при Е=5% ЧДД=3,29 млн. руб., а при Е=8% ЧДД = -25,22 млн. руб.
ВНД = 5 – 3,29 · ((8-5)/(-25,22 – 3,29)) = 5,35%.
Этой формулой можно пользоваться в случае, если Е1 и Е2 различаются не больше чем на 3%. В противном случае получается большая погрешность. Если же эта разность превышает 3%, то ВНД определяется методом итерации, при кот. ВНД определяется серией попыток расчета ЧДД при разных ставках Е до тех пор, пока ЧДД станет отрицательным.
Затем строится график в осях координат ЧДД и Е, где кривая пересечет ось абсцисс.
Расчет ВНД.
При Е=10% ЧДД = 162,27 млн. руб.
Задаем Е=20%
ЧДД: 100 : (1 + 0,2) + 150 : 1,22 = 187, 497 млн. руб.
ЧДД = 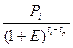 = 100 : 1,11 + 150 : 1,12 = 90,9 = 50 : 1,23 + 150 : 1,24 + 200 : 1,25 + 200 : 1,26 = 248,66 млн. руб.
= 100 : 1,11 + 150 : 1,12 = 90,9 = 50 : 1,23 + 150 : 1,24 + 200 : 1,25 + 200 : 1,26 = 248,66 млн. руб.
ЧДД = 248,66 – 187,497 = 61,16 млн. руб.
Далее Е = 30% 100 : 1,31 + 150 : 1,32 = 165,168 млн. руб.
50 : 1,33 + 150 : 1,34 + 200 : 1,35 = 200 : 1,36 = 170,59 млн. руб.
ЧДД = 170,59 – 165,168 = 4,91
Далее строим график:
ЧДД, млн. руб.
Е, %

Показатель ВНД хар-ет примерную величину предела безопасности для проекта.
Дата добавления: 2015-07-22; просмотров: 665;
