Ферментативный катализ

Первые количественные результаты по кинетике ферментативных реакций были получены в начале ХХ в. В 1913 г. для их объяснения Л. Михаэлис предложил схему превращений с образованием промежуточных соединений в результате создания полноценной связи между субстратом S и ферментом, или энзимом E , действующим на этот субстрат.

Разработанная теория получила название главновалентной. Она предполагает, что фермент с субстратом могут образовывать комплекс, который способен распадаться как с образованием продуктов реакции, так и с образованием исходного вещества. Схема превращений может быть записана следующим образом:

k₁ k₂

S + E D ES ® E + P,

k₋₁

где ES - комплекс, образуемый ферментом и субстратом.

Обозначив концентрации всех веществ, приведенных в схеме, через [S], [E] и [ES], запишем уравнение для скорости накопления фермент-субстратного комплекса:

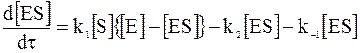. (16 - 2)

^{концентрация}

^{несвязанного}

^{фермента}

При записи уравнения (16 - 2) специально отмечено, что в реакции с субстратом участвует только та часть фермента, которая не связана с субстратом в комплексе.

Начало ферментативной реакции сопровождается очень быстрым ростом концентрации фермент-субстратного комплекса, а затем после достижения максимума его концентрация медленно падает. Таким образом, по сравнению с начальной частью кинетической кривой после достижения максимума можно принять производную концентрации фермент-субстратного комплекса по времени очень малой, то есть . Подобный случай накопления промежуточного соединения уже рассматривался при объяснении первого порядка реакции по схеме Линдемана. Состояние после достижения максимума на кинетической кривой промежуточного соединения называется квазистационарным состоянием.Используя условие квазистационарного состояния, запишем:

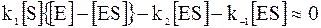. (16 - 3)

В условиях квазистационарного состояния концентрация фермент-субстратного комплекса равна:

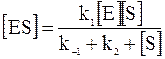. (16 - 4)

Принимая, что скорость реакции в целом определяется скоростью образования продукта реакции по второй стадии:

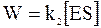, (16 - 5)

получим зависимость скорости реакции от концентраций фермента и субстрата:

. (16 - 6)

Число констант в уравнении (16 - 6) можно уменьшить, введя новую величину

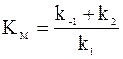. (16 - 7)

Величина K_M называется константой Михаэлиса. Константа Михаэлиса является индивидуальной характеристикой фермента. Ее размерность совпадает с размерностью концентрации. Значения константы Михаэлиса находятся в очень широких пределах и могут составлять от десятка до сотых долей ммоль/л.

С введением константы Михаэлиса уравнение (16 - 6) принимает более простой вид:

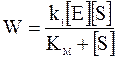. (16 - 8)

Уравнению (16 - 8) можно придать другую форму, для чего рассмотрим условие: [S] >> K_M. В этом случае скорость реакции достигает максимального значения W_max.

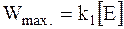(16 - 9)

и перестает зависеть от концентрации субстрата. Следовательно, этому условию отвечает реакция нулевого порядка по субстрату.

Рис. 16 - 2. Зависимость скорости фер­ментативной реакции от концентрации субстрата.

Используя равенство (16 - 9), получим окончательную форму уравнения, описывающего кинетику ферментативных реакций:

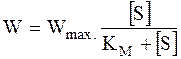. (16 - 10)

Уравнение (16 - 10) называется уравнением Михаэлиса - Ментен.

Зависимость скорости ферментативной реакции от концентрации субстрата показана на рис. 16 - 2.

Для нахождения максимальной скорости ферментативной реакции и константы Михаэлиса уравнение Михаэлиса - Ментен преобразуют следующим образом:

Рис. 16 - 3. Графическое опреде­ление констант уравнения Миха­элиса ‑ Ментен.

. (16 - 11)

Графические методы определения констант уравнения Михаэлиса - Ментен показаны на рис. 16 ‑ 3.

Ферменты являются наиболее специфическими и активными катализаторами из всех известных.

Влияние различных факторов (рН, солей и других веществ, температуры) на активность ферментов изучается в курсе биохимии.