Два случая бимолекулярной реакции

Возможные случаи бимолекулярной реакции можно представить следующим образом:

1) 2A ¾® Продукты реакции,

2) A + B ¾® Продукты реакции.

Первый случай описывается уравнениями (9 - 21) и (9 - 23). При равенстве концентраций веществ A и B также применимы уравнения (9 - 21) и (9 - 23).

Если концентрации веществ А и В не равны (С_А ≠ С_В), то применяется другое уравнение, для вывода которого используем следующие условия.

Пусть к началу реакции концентрация вещества А и концентрация вещества В соответственно равны a и b, а к моменту времени t концентрация вещества уменьшится на х и станет равной C_A = a – x. В соответствии с уравнением реакции концентрация вещества В также уменьшится на х и окажется равной C_B = b − x. Кинетическое уравнение примет следующий вид:

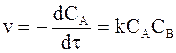(9 - 27)

или

;

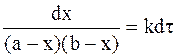. (9 - 28)

При интегрировании уравнения (9 - 28) воспользуемся известным из курса математического анализа методом неопределенных коэффициентов, согласно которому дробь, входящую в левую часть равенства (9 - 28), можно представить суммой двух дробей, содержащих неопределенные множители a и b:

.

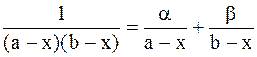Проведя очевидные преобразования, получим:

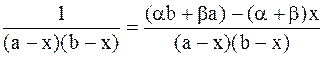. (9 - 29)

Так как в числителе левой части равенства (9 - 29) не содержится х, то

a + b = 0, (а)

а равенство числителя левой части 1 означает:

ab + ba = 1. (b)

Из условий (a) и (b) следует, что неопределенные коэффициенты равны:

, .

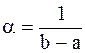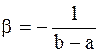Интегрирование уравнения (9 - 28) дает:

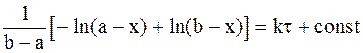. (9 - 30)

Граничные условия (х = 0 при t = 0) позволяют найти постоянную интегрирования:

.

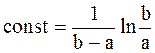Окончательный вид уравнения, описывающего кинетику бимолекулярной необратимой реакции с разными исходными концентрациями веществ, таков:

. (9 - 31)

Нетрудно заметить, что прямая подстановка в уравнение (9 ‑ 31) равных исходных концентраций (a = b) приводит к неопределенности типа .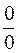

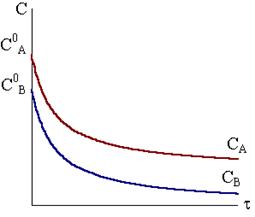Рис. 9 - 4. Кинетические кривые веществ в случае реакции А+В ® Продукты при неравных исходных концентрациях веществ.

На рис. 9 - 4 показаны кинетические кривые обоих веществ. Расстояние между ними по ординате всегда остается постоянным и по абсолютной величине равным разности исходных концентраций ça - bç.