Логико-термальная эквивалентность

Отношение эквивалентности Е, заданное на парах стандартных схем, называют корректным, если для любой пары схем S₁ и S₂ из S₁ ~Е~ S₂ следует, что S₁~ S₂, т. е. S₁ и S₂ функционально эквивалентны.

Поиск разрешимых корректных отношений эквивалентности представляет значительный интерес с точки зрения практической оптимизации преобразования программ, поскольку в общем виде функциональная эквивалентность стандартных схем алгоритмически неразрешима.

Идея построения таких (корректных и разрешимых) отношений связанна с введением понятия истории цепочки схем. В истории с той или иной степенью детальности фиксируются промежуточные результаты выполнения операторов рассматриваемой цепочки. Эквивалентными объявляются схемы, у которых совпадают множества историй всех конечных цепочек.

Одним из отношений эквивалентности является логико-термальная эквивалентность (ЛТЭ).

Определим термальное значение переменной х для конечного пути w схемы S как терм t(w, x), который строится следующим образом.

1.Если путь w содержит только один оператор А, то: t(w, x) = t, если А – оператор присваивания, t(w, x) = х, в остальных случаях.

2.Если w = w’Ае, где А – оператор, е – выходящая из него дуга, w’ – непустой путь, ведущий к А, а x₁, …, x_n – все переменные терма t(Ае, x), то t(w, x) = t(Ае, x)[t(w’, x₁)/x₁, …, t(w’, x_n)/x_n].

Понятие термального значения распространим на произвольные термы t:

t(w, x) = t [t(w, x₁)/x₁, …, t(w, x_n)/x_n].

Например, путиstart(х); y:=x; p¹(x); x:=f(x); p⁰(y); y:=x; p¹(x); x:=f(x) в схеме на рисунке 1.5, а соответствует термальное значение f(f(x)) переменной х.

Для пути w в стандартной схеме S определим ее логико-термальную историю (ЛТИ) lt(S, w) как слово, которое строится следующим образом.

1.Если путь w не содержит распознавателей и заключительной вершины, то lt(S, w) – пустое слово.

2.Если w = w’vе, где v – распознаватель с тестом p(t₁, ..., t_k), а е – выходящая из него Δ-дуга, Δ {0,1}, то

lt(S, w) = lt(S, w’) p^Δ(t(w’, t₁), …, t(w’, t_k)).

3.Если w = w’v, где v – заключительная вершина с оператором stop(t₁, ..., t_k), то lt(S, w) = lt(S, w’) t(w’, t₁) … t(w’, t_k).

Например, логико-термальной историей пути, упомянутого в приведенном выше примере, будет p¹(x) p⁰(x) p¹(f(x)).

Детерминантом (обозначение: det(S)) стандартной схемы S называют множество ЛТИ всех ее цепочек, завершающихся заключительным оператором.

Схемы S₁ и S₂ называют ЛТЭ (лт - эквивалентными) S₁ ~ЛТ~ S₂, если их детерминанты совпадают.

Приведем без доказательства следующие утверждение:

Логико-терминальная эквивалентность корректна, т. е. из ЛТЭ следует функциональная эквивалентность (S₁ ~ЛТ~ S₂ 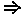S₁ ~ S₂). Обратное утверждение как видно из рисунка 1.5 не верно.

ЛТ – эквивалентность допускает меньше сохраняющих ее преобразований, чем функциональная эквивалентность.