Многоленточные автоматы

Многоленточный (детерминированный, односторонний) конечный автомат (МКА) задается так же, как ОКА. Отличие состоит в том, что множество состояний Q разбивается на n ³ 2 подмножеств (непересекающихся) Q₁, ..., Q_n. «Физическая» интерпретация n - ленточного автомата отличается тем, что он имеет n лент и n головок, по головке на ленту. Если автомат находится в состоянии q Q_i, то i-я головка читает i-ю ленту так же, как это делает ОКА. При переходе МКА в состояние q' Q_j (i 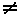j) i-я головка останавливается, а j-я начинает читать свою ленту. МКА останавливается, когда головка на одной из лент прочитает символ #.

Рассмотрим функционирование МКА с n = 2 (рисунок 1.7.) на примере сравнения пар слов в алфавите {1, 0} и допуске только совпадающих слов.

Здесь Q = Q₁ 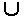Q₂, где Q₁={q₀¹}; Q₂={q₁², q₂², q₃²}; R={q₀¹}; V={0, 1}, начальное состояние - q₀¹. МКА обрабатывает наборы слов (U₁, U₂), где слово U₁ записано на первой ленте, а U₂ - на второй. Допустимое множество наборов M_A -это все возможные пары одинаковых слов, т.е. наборы, где U₁ = U₂. Например, набор может быть (1101, 1101) и т.п.

В том случае, когда слова совпадают, МКА остановится в заключительном состоянии q₀¹ (именно в этом состоянии поступит символ #) и набор будет допущен. Если слова не совпадут хотя бы в одном символе, МКА перейдет в состояние q₃², из которого не выйдет до появления символа #, который и зафиксирует отсутствие совпадения слов, т.е. не допустит искаженный набор.

Доказана разрешимость проблемы эквивалентности двухленточных автоматов.